题目内容
10.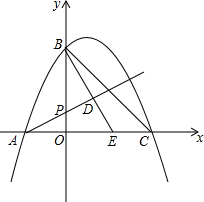 已知在平面直角坐标系xOy(如图)中,抛物线y=-x2+bx+c与x轴交于点A(-1,0)与点C(3,0),与y轴交于点B,点P为OB上一点,过点B作射线AP的垂线,垂足为点D,射线BD交x轴于点E.
已知在平面直角坐标系xOy(如图)中,抛物线y=-x2+bx+c与x轴交于点A(-1,0)与点C(3,0),与y轴交于点B,点P为OB上一点,过点B作射线AP的垂线,垂足为点D,射线BD交x轴于点E.(1)求该抛物线的解析式;
(2)连结BC,当P点坐标为(0,$\frac{2}{3}$)时,求△EBC的面积;
(3)当点D落在抛物线的对称轴上时,求点P的坐标.
分析 (1)将A、C点的坐标代入抛物线解析式,得到关于b、c的二元一次方程,解方程即可得出结论;
(2)由∠APO、∠AED均匀∠PAO互余得出∠APO=∠AED,再结合∠AOP=∠BOE=90°可得出△AOP∽△BOE,由相似三角形的性质得出$\frac{OE}{OP}=\frac{OB}{OA}$,代入数据可得出OE的长度,结合C点坐标可得出CE长度,将CE、OB的长度代入三角形的面积公式,即可得出结论;
(3)令对称轴与x轴的交点为H,过点B作BF⊥直线x=1于点F,先证△ADH∽△DBF,再由相似三角形的性质找出$\frac{AH}{DF}=\frac{HD}{FB}$,设DH=a,由此可得出关于a的一元二次方程,解方程可求出a的值,再根据$\frac{OP}{HD}=\frac{AO}{AH}=\frac{1}{2}$可得出OP的长度,从而得出P点的坐标.
解答 解:(1)将点A(-1,0),点C(3,0)的坐标代入抛物线解析式,得:$\left\{\begin{array}{l}{0=-1-b+c}\\{0=-9+3b+c}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{b=2}\\{c=3}\end{array}\right.$.
故该抛物线的解析式为y=-x2+2x+3.
(2)∵BD⊥AD,
∴∠ADE=90°,
∴∠PAO+∠APO=∠PAO+∠AED=90°,
∴∠APO=∠AED=∠BEO,
又∵∠AOP=∠BOE=90°,
∴△AOP∽△BOE,
∴$\frac{OE}{OP}=\frac{OB}{OA}$.
令x=0,y=3,即点B的坐标为(0,3),
∵点A(-1,0),点C(3,0),点P(0,$\frac{2}{3}$),
∴OE=2,
∴CE=OC-OE=3-2=1.
S△EBC=$\frac{1}{2}$CE•OB=$\frac{3}{2}$.
(3)抛物线对称轴直线x=-$\frac{2}{-1}$=1,令对称轴与x轴的交点为H,过点B作BF⊥直线x=1于点F,如图所示.
∵DH⊥x轴,BF⊥FD,
∴∠AHD=∠DFB=90°,
∵∠BDF+∠BDA+∠ADH=180°,∠BDA=90°,∠BDF+∠DBF=90°,
∴∠ADH=∠DBF,
∴△ADH∽△DBF,
∴$\frac{AH}{DF}=\frac{HD}{FB}$.
设DH=a.
∵AH=2,DF=BO-DH=3-a,FB=1,
∴有$\frac{2}{3-a}=\frac{a}{1}$,
解得:a1=1,a2=2.
又∵$\frac{OP}{HD}=\frac{AO}{AH}=\frac{1}{2}$,
∴OP=$\frac{1}{2}$或1.
故点P的坐标为(0,1)或(0,$\frac{1}{2}$).
点评 本题考查了待定系数法求函数解析式、相似三角形的判定及性质、解一元二次方程,解题的关键:(1)待定系数法求解析式的系数;(2)找出线段CE的长度;(3)由相似三角形的性质找出关于a的一元二次方程.本题属于中档题,(1)难度不大;(2)(3)有点难度.解决该类问题,利用相似三角形的性质找出比例关系,解方程即可得出结论.

 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案 如图,在?ABCD中,AE⊥BC,垂足为E,如果AB=5,BC=8,sinB=$\frac{4}{5}$,那么tan∠CDE的值为( )
如图,在?ABCD中,AE⊥BC,垂足为E,如果AB=5,BC=8,sinB=$\frac{4}{5}$,那么tan∠CDE的值为( )| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\sqrt{2}-1$ |
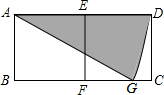 如图,两个小正方形的边长都是1,以A为圆心,AD为半径作弧交BC于点G,则图中阴影部分的面积为( )
如图,两个小正方形的边长都是1,以A为圆心,AD为半径作弧交BC于点G,则图中阴影部分的面积为( )| A. | $\frac{π}{3}$ | B. | $\frac{2π}{3}$ | C. | $\frac{π}{6}$ | D. | $\frac{π}{2}$ |
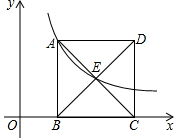 如图,正方形ABCD的边长为4,边BC在x轴上,点E是对角线AC,BD的交点,反比例函数y=$\frac{k}{x}(x>0)$的图象经过A,E两点,则k的值为( )
如图,正方形ABCD的边长为4,边BC在x轴上,点E是对角线AC,BD的交点,反比例函数y=$\frac{k}{x}(x>0)$的图象经过A,E两点,则k的值为( )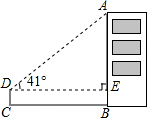 如图,某校教学兴趣小组为测量建筑物AB的高度,用高度为1m的测量仪器CD,在距建筑物AB底部25m的C处,测得该建筑物顶部A处的仰角为∠ADE=41°,求建筑物AB的高度.(精确到0.1m).
如图,某校教学兴趣小组为测量建筑物AB的高度,用高度为1m的测量仪器CD,在距建筑物AB底部25m的C处,测得该建筑物顶部A处的仰角为∠ADE=41°,求建筑物AB的高度.(精确到0.1m). 如图,为了测量教学楼前一棵大树的高度,王明和王亮拿自制的测倾器分别在教学楼AH的二楼C处测得树顶E的仰角为30°,在四楼B处测得大树底部D点的俯角为45°.已知二楼C处离地面高4米,四楼B处离地面高12米.试求树高DE.(参考数据:$\sqrt{3}$≈1.73,结果保留一位小数)
如图,为了测量教学楼前一棵大树的高度,王明和王亮拿自制的测倾器分别在教学楼AH的二楼C处测得树顶E的仰角为30°,在四楼B处测得大树底部D点的俯角为45°.已知二楼C处离地面高4米,四楼B处离地面高12米.试求树高DE.(参考数据:$\sqrt{3}$≈1.73,结果保留一位小数) 如图,在△ABC中,∠A=40°,∠B=72°,CD是AB边上的高,CE是∠ACB的平分线,DF⊥CE于F,求∠CDF的度数.
如图,在△ABC中,∠A=40°,∠B=72°,CD是AB边上的高,CE是∠ACB的平分线,DF⊥CE于F,求∠CDF的度数.