题目内容
14.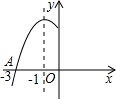 如图,是二次函数y=ax2+bx+c图象的一部分,图象过点A(-3,0),对称轴为x=-1,给出四个结论:
如图,是二次函数y=ax2+bx+c图象的一部分,图象过点A(-3,0),对称轴为x=-1,给出四个结论:①b2>4ac;②2a-b=0;③a+b+c=0;④5a<b.
其中正确结论的个数是( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 由抛物线的开口向下知a<0,与y轴的交点在y轴的正半轴上得到c>0,由对称轴为x=-$\frac{b}{2a}$=-1可以判定②;由图象与x轴有交点,对称轴为x=-$\frac{b}{2a}$=-1,与y轴的交点在y轴的正半轴上,可以推出b2-4ac>0,即b2>4ac,即可判定①;由x=1时y=0,即可判定③.把x=1,x=-3代入解析式得a+b+c=0,9a-3b+c=0,两边相加整理即可判定④.
解答 解:①∵图象与x轴有交点,对称轴为x=-$\frac{b}{2a}$=-1,与y轴的交点在y轴的正半轴上,
又∵二次函数的图象是抛物线,
∴与x轴有两个交点,
∴b2-4ac>0,
即b2>4ac,正确;
②∵对称轴为x=-$\frac{b}{2a}$=-1,
∴2a=b,
∴2a-b=0,正确;
③∵抛物线的一个交点为(-3,))对称轴为x=-1,
∴另一个交点为(1,0),
∴当x=1时,y=a+b+c=0,正确;
④把x=1,x=-3代入解析式得a+b+c=0,9a-3b+c=0,两边相加整理得
5a-b=-c<0,即5a<b,正确.
故正确的为①②③④,
故选D.
点评 解答本题关键是掌握二次函数y=ax2+bx+c系数符号由抛物线开口方向、对称轴、抛物线与y轴的交点、抛物线与x轴交点的个数确定.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
4.下列命题中,是真命题的是( )
| A. | 长度相等的两条弧是等弧 | |
| B. | 顺次连结平行四边形四边中点所组成的图形是菱形 | |
| C. | 正八边形既是轴对称图形又是中心对称图形 | |
| D. | 三角形的内心到这个三角形三个顶点的距离相等 |
 如图,为了测量教学楼前一棵大树的高度,王明和王亮拿自制的测倾器分别在教学楼AH的二楼C处测得树顶E的仰角为30°,在四楼B处测得大树底部D点的俯角为45°.已知二楼C处离地面高4米,四楼B处离地面高12米.试求树高DE.(参考数据:$\sqrt{3}$≈1.73,结果保留一位小数)
如图,为了测量教学楼前一棵大树的高度,王明和王亮拿自制的测倾器分别在教学楼AH的二楼C处测得树顶E的仰角为30°,在四楼B处测得大树底部D点的俯角为45°.已知二楼C处离地面高4米,四楼B处离地面高12米.试求树高DE.(参考数据:$\sqrt{3}$≈1.73,结果保留一位小数)
 如图,已知△ABC是⊙O的内接三角形,直线CD是⊙O的切线,AC平分∠BAD.
如图,已知△ABC是⊙O的内接三角形,直线CD是⊙O的切线,AC平分∠BAD.