题目内容
9.A、B、C三张外观一样的门卡可分别对应a、b、c三把电子锁,若任意取出其中一张门卡,恰好打开a锁的概率是$\frac{1}{3}$;若随机取出三张门卡,恰好一次性对应打开这三把电子锁的概率是$\frac{1}{6}$.分析 直接利用概率公式求任意取出其中一张门卡,恰好打开a锁的概率;画树状图展示所有6种等可能的结果数,找出恰好一次性对应打开这三把电子锁的结果数,然后根据概率公式求解.
解答 解:若任意取出其中一张门卡,恰好打开a锁的概率是$\frac{1}{3}$;
画树状图为:
共有6种等可能的结果数,恰好一次性对应打开这三把电子锁的结果数为1,
所以恰好一次性对应打开这三把电子锁的概率为$\frac{1}{6}$.、
故答案为$\frac{1}{3}$,$\frac{1}{6}$.
点评 本题考查了列表法与树状图法:利用列表法和树状图法展示所有可能的结果求出n,再从中选出符合事件A或B的结果数目m,求出概率.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
20. 如图,在?ABCD中,AE⊥BC,垂足为E,如果AB=5,BC=8,sinB=$\frac{4}{5}$,那么tan∠CDE的值为( )
如图,在?ABCD中,AE⊥BC,垂足为E,如果AB=5,BC=8,sinB=$\frac{4}{5}$,那么tan∠CDE的值为( )
 如图,在?ABCD中,AE⊥BC,垂足为E,如果AB=5,BC=8,sinB=$\frac{4}{5}$,那么tan∠CDE的值为( )
如图,在?ABCD中,AE⊥BC,垂足为E,如果AB=5,BC=8,sinB=$\frac{4}{5}$,那么tan∠CDE的值为( )| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\sqrt{2}-1$ |
4.下列命题中,是真命题的是( )
| A. | 长度相等的两条弧是等弧 | |
| B. | 顺次连结平行四边形四边中点所组成的图形是菱形 | |
| C. | 正八边形既是轴对称图形又是中心对称图形 | |
| D. | 三角形的内心到这个三角形三个顶点的距离相等 |
14.已知反比例函数的图象经过点(-2,4),当x=4时,所对应的函数值y等于( )
| A. | 2 | B. | -2 | C. | 4 | D. | -4 |
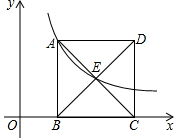 如图,正方形ABCD的边长为4,边BC在x轴上,点E是对角线AC,BD的交点,反比例函数y=$\frac{k}{x}(x>0)$的图象经过A,E两点,则k的值为( )
如图,正方形ABCD的边长为4,边BC在x轴上,点E是对角线AC,BD的交点,反比例函数y=$\frac{k}{x}(x>0)$的图象经过A,E两点,则k的值为( )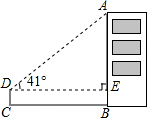 如图,某校教学兴趣小组为测量建筑物AB的高度,用高度为1m的测量仪器CD,在距建筑物AB底部25m的C处,测得该建筑物顶部A处的仰角为∠ADE=41°,求建筑物AB的高度.(精确到0.1m).
如图,某校教学兴趣小组为测量建筑物AB的高度,用高度为1m的测量仪器CD,在距建筑物AB底部25m的C处,测得该建筑物顶部A处的仰角为∠ADE=41°,求建筑物AB的高度.(精确到0.1m).