题目内容
4.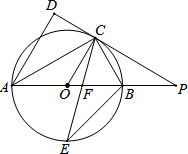 如图,AB是⊙O的直径,点C是⊙O上一点,AD与过点C的切线垂直,垂足为点D,直线DC与AB的延长线相交于点P,弦CE平分∠ACB,交AB于点F,连接BE.
如图,AB是⊙O的直径,点C是⊙O上一点,AD与过点C的切线垂直,垂足为点D,直线DC与AB的延长线相交于点P,弦CE平分∠ACB,交AB于点F,连接BE.(1)求证:△PCF是等腰三角形;
(2)若tan∠ABC=$\frac{4}{3}$,BE=$\frac{7\sqrt{2}}{2}$,求线段PC的长.
分析 (1)根据圆周角定理得∠ACB=90°,则∠ACF=∠BCF=45°,再根据切线的性质得∠PCB+∠OCB=90°,加上∠OCB=∠OBC,∠OBC+∠BAC=90°,则∠PCB=∠BAC,然后根据三角形外角性质可证明∠PCF=∠PFC,
于是利用等腰三角形的判定定理可得△PCF是等腰三角形;
(2)连结AE,如图,先证明△ABE为等腰直角三角形得到AB=$\sqrt{2}$BE=7,再在Rt△ACB中,利用正切定义得tan∠ABC=$\frac{AC}{BC}$=$\frac{4}{3}$,则可设AC=4x,BC=3x,所以AB=5x=7,解得x=$\frac{7}{5}$,即AC=$\frac{28}{5}$,BC=$\frac{21}{5}$,接着证明Rt△DAC∽Rt△CAB,利用相似比可计算出AD=$\frac{112}{25}$,DC=$\frac{84}{25}$,然后利用OP∥AD得到△POC∽△PAD,则可利用相似比计算出PC的长.
解答 (1)证明:∵AB是⊙O的直径,
∴∠ACB=90°,
∵弦CE平分∠ACB,
∴∠ACF=∠BCF=45°,
∵PC为⊙O的切线,
∴OC⊥PC,
∴∠PCO=90°,即∠PCB+∠OCB=90°,
而OC=OB,
∴∠OCB=∠OBC,
而∠OBC+∠BAC=90°,
∴∠PCB=∠BAC,
∵∠PCF=∠PCB+∠BCF=∠PCB+45°,∠PFC=∠FAC+∠ACF=∠BAC+45°,
∴∠PCF=∠PFC,
∴△PCF是等腰三角形;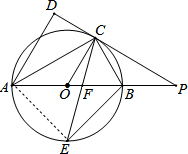
(2)解:连结AE,如图,
∵∠ABE=∠ACE=45°,∠BAE=∠BCE=45°,
∴△ABE为等腰直角三角形,
∴AB=$\sqrt{2}$BE=$\sqrt{2}$×$\frac{7\sqrt{2}}{2}$=7,
在Rt△ACB中,tan∠ABC=$\frac{AC}{BC}$=$\frac{4}{3}$,
设AC=4x,BC=3x,则AB=5x,
∴5x=7,解得x=$\frac{7}{5}$,
∴AC=$\frac{28}{5}$,BC=$\frac{21}{5}$,
∵AD⊥CD,OC⊥CD,
∴OC∥AD,
∴∠DAC=∠ACO,
而∠ACO=∠OAC,
∴∠DAC=∠BAC,
∴Rt△DAC∽Rt△CAB,
∴$\frac{AD}{AC}$=$\frac{DC}{BC}$=$\frac{AC}{AB}$,即$\frac{AD}{\frac{28}{5}}$=$\frac{DC}{\frac{21}{5}}$=$\frac{\frac{28}{5}}{7}$,
∴AD=$\frac{112}{25}$,DC=$\frac{84}{25}$,
∵OP∥AD,
∴△POC∽△PAD,
∴$\frac{PC}{PD}$=$\frac{OC}{AD}$,即$\frac{PC}{PC+\frac{84}{25}}$=$\frac{\frac{7}{2}}{\frac{112}{25}}$,
∴PC=12.
点评 本题考查了切线的性质:圆的切线垂直于经过切点的半径.也考查圆周角定理和相似三角形的判定与性质.

| A. | 8个 | B. | 7个 | C. | 5个 | D. | 6个 |
 如图,△ABC中,AC=BC,点D在线段AB上,CE∥AB,且CE=BD.
如图,△ABC中,AC=BC,点D在线段AB上,CE∥AB,且CE=BD. 如图,已知:在四边形ABFC中,∠ACB=90°,BC的垂直平分线EF交BC于点D,交AB于点E,且CF=AE;
如图,已知:在四边形ABFC中,∠ACB=90°,BC的垂直平分线EF交BC于点D,交AB于点E,且CF=AE;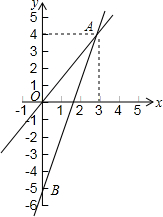 如图,一个正比例函数与一个一次函数的图象交于点A(3,4),其中一次函数与y轴交于B点,且OA=OB.
如图,一个正比例函数与一个一次函数的图象交于点A(3,4),其中一次函数与y轴交于B点,且OA=OB. (1)某水果批发商,批发苹果不少于80kg时,批发价为2.5元/kg,小张携现金2500元到这个市场采购苹果,并以批发价买进,设购买的苹果为xkg,小张付款后还剩余现金y元,写出y与x的函数关系式,并指出自变量x的取值范围.
(1)某水果批发商,批发苹果不少于80kg时,批发价为2.5元/kg,小张携现金2500元到这个市场采购苹果,并以批发价买进,设购买的苹果为xkg,小张付款后还剩余现金y元,写出y与x的函数关系式,并指出自变量x的取值范围.