题目内容
9.化简:($\frac{a}{a-b}$-$\frac{{b}^{2}}{{a}^{2}-ab}$)÷$\frac{{a}^{2}+2ab+{b}^{2}}{a}$,当a=1,b=-2时,求代数式的值.分析 先根据分式混合运算的法则把原式进行化简,再把a,b的值进行计算即可.
解答 解:原式=($\frac{a}{a-b}$-$\frac{{b}^{2}}{a(a-b)}$)•$\frac{a}{(a+b)^{2}}$
=$\frac{(a+b)(a-b)}{a(a-b)}$•$\frac{a}{{(a+b)}^{2}}$
=$\frac{1}{a+b}$,
当a=1,b=-2时,原式=$\frac{1}{1-2}$=-1.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
相关题目
2.两数和为负数,那么这两数必定是( )
| A. | 同为正数 | B. | 同为负数 | ||
| C. | 一个为零一个为负数 | D. | 至少一个为负数,且负数绝对值大 |
17.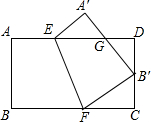 如图,将矩形纸片ABCD沿EF折叠,使点B与CD的中点B′重合,若AB=2,BC=3,则△FCB′与△B′DG的面积之比为( )
如图,将矩形纸片ABCD沿EF折叠,使点B与CD的中点B′重合,若AB=2,BC=3,则△FCB′与△B′DG的面积之比为( )
 如图,将矩形纸片ABCD沿EF折叠,使点B与CD的中点B′重合,若AB=2,BC=3,则△FCB′与△B′DG的面积之比为( )
如图,将矩形纸片ABCD沿EF折叠,使点B与CD的中点B′重合,若AB=2,BC=3,则△FCB′与△B′DG的面积之比为( )| A. | 9:4 | B. | 3:2 | C. | 16:9 | D. | 4:3 |
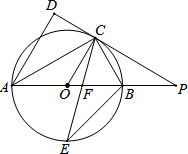 如图,AB是⊙O的直径,点C是⊙O上一点,AD与过点C的切线垂直,垂足为点D,直线DC与AB的延长线相交于点P,弦CE平分∠ACB,交AB于点F,连接BE.
如图,AB是⊙O的直径,点C是⊙O上一点,AD与过点C的切线垂直,垂足为点D,直线DC与AB的延长线相交于点P,弦CE平分∠ACB,交AB于点F,连接BE.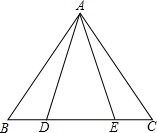 如图,△ABC中,点D、E在BC边上,∠BAD=∠CAE请你添加一对相等的线段或一对相等的角的条件,使△ABD≌△ACE.你所添加的条件是AB=AC.
如图,△ABC中,点D、E在BC边上,∠BAD=∠CAE请你添加一对相等的线段或一对相等的角的条件,使△ABD≌△ACE.你所添加的条件是AB=AC.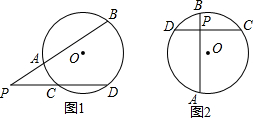 (1)如图所示,点P在⊙O外,过点P作两射线,分别与⊙O相交于点A、B、C、D,猜想$\widehat{AB}$的度数、$\widehat{CD}$的度数与∠P之间的数量关系,并进行证明.
(1)如图所示,点P在⊙O外,过点P作两射线,分别与⊙O相交于点A、B、C、D,猜想$\widehat{AB}$的度数、$\widehat{CD}$的度数与∠P之间的数量关系,并进行证明.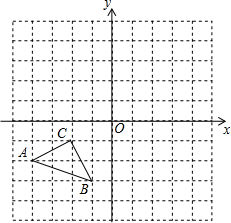 已知△ABC各顶点的坐标为A(-4,-2),B(-1,-3),C(-2,-1),将△ABC先向右平移4个单位长度,再向上平移3个单位长度得到△A′B′C′.
已知△ABC各顶点的坐标为A(-4,-2),B(-1,-3),C(-2,-1),将△ABC先向右平移4个单位长度,再向上平移3个单位长度得到△A′B′C′.