题目内容
13.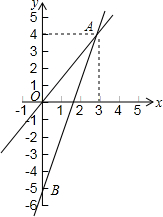 如图,一个正比例函数与一个一次函数的图象交于点A(3,4),其中一次函数与y轴交于B点,且OA=OB.
如图,一个正比例函数与一个一次函数的图象交于点A(3,4),其中一次函数与y轴交于B点,且OA=OB.(1)求这两个函数的表达式;
(2)求△AOB的面积S.
分析 (1)把A点坐标代入可先求得直线OA的解析式,可求得OA的长,则可求得B点坐标,可求得直线AB的解析式;
(2)由A点坐标可求得A到y轴的距离,根据三角形面积公式可求得S.
解答 解:
(1)设直线OA的解析式为y=kx,
把A(3,4)代入得4=3k,解得k=$\frac{4}{3}$,
所以直线OA的解析式为y=$\frac{4}{3}$x;
∵A点坐标为(3,4),
∴OA=$\sqrt{{3}^{2}+{4}^{2}}$=5,
∴OB=OA=5,
∴B点坐标为(0,-5),
设直线AB的解析式为y=ax+b,
把A(3,4)、B(0,-5)代入得$\left\{\begin{array}{l}{3a+b=4}\\{b=-5}\end{array}\right.$,解得$\left\{\begin{array}{l}{a=3}\\{b=-5}\end{array}\right.$,
∴直线AB的解析式为y=3x-5;
(2)∵A(3,4),
∴A点到y轴的距离为3,且OB=5,
∴S=$\frac{1}{2}$×5×3=$\frac{15}{2}$.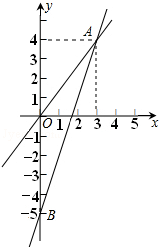
点评 本题主要考查一次函数的交点问题,掌握两函数图象的交点坐标满足两函数解析式是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.下列各曲线表示的y与x的关系中,y不是x的函数的是( )
| A. | 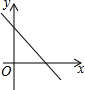 | B. | 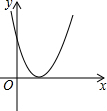 | ||
| C. | 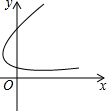 | D. | 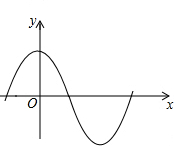 |
3.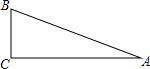 如图,在Rt△ABC中,∠C=90°,AC=6,BC=2,则cosA的值为( )
如图,在Rt△ABC中,∠C=90°,AC=6,BC=2,则cosA的值为( )
 如图,在Rt△ABC中,∠C=90°,AC=6,BC=2,则cosA的值为( )
如图,在Rt△ABC中,∠C=90°,AC=6,BC=2,则cosA的值为( )| A. | $\frac{\sqrt{10}}{10}$ | B. | $\frac{3\sqrt{10}}{10}$ | C. | $\frac{1}{3}$ | D. | 3 |
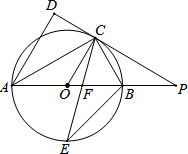 如图,AB是⊙O的直径,点C是⊙O上一点,AD与过点C的切线垂直,垂足为点D,直线DC与AB的延长线相交于点P,弦CE平分∠ACB,交AB于点F,连接BE.
如图,AB是⊙O的直径,点C是⊙O上一点,AD与过点C的切线垂直,垂足为点D,直线DC与AB的延长线相交于点P,弦CE平分∠ACB,交AB于点F,连接BE.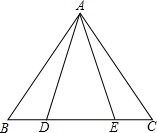 如图,△ABC中,点D、E在BC边上,∠BAD=∠CAE请你添加一对相等的线段或一对相等的角的条件,使△ABD≌△ACE.你所添加的条件是AB=AC.
如图,△ABC中,点D、E在BC边上,∠BAD=∠CAE请你添加一对相等的线段或一对相等的角的条件,使△ABD≌△ACE.你所添加的条件是AB=AC.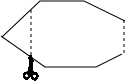 如图,一个多边形纸片按图示的剪法剪去一个内角后,得到一个内角和为2340°的新多边形,则原多边形的边数为14.
如图,一个多边形纸片按图示的剪法剪去一个内角后,得到一个内角和为2340°的新多边形,则原多边形的边数为14.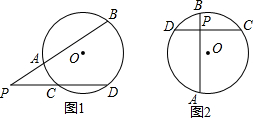 (1)如图所示,点P在⊙O外,过点P作两射线,分别与⊙O相交于点A、B、C、D,猜想$\widehat{AB}$的度数、$\widehat{CD}$的度数与∠P之间的数量关系,并进行证明.
(1)如图所示,点P在⊙O外,过点P作两射线,分别与⊙O相交于点A、B、C、D,猜想$\widehat{AB}$的度数、$\widehat{CD}$的度数与∠P之间的数量关系,并进行证明.