题目内容
19. 如图,已知:在四边形ABFC中,∠ACB=90°,BC的垂直平分线EF交BC于点D,交AB于点E,且CF=AE;
如图,已知:在四边形ABFC中,∠ACB=90°,BC的垂直平分线EF交BC于点D,交AB于点E,且CF=AE;(1)试判断四边形BECF是什么四边形?并说明理由.
(2)当∠A的大小满足什么条件时,四边形BECF是正方形?请回答并证明你的结论.
分析 (1)根据中垂线的性质:中垂线上的点到线段两个端点的距离相等,有BE=EC,BF=FC,又因为CF=AE,BE=EC=BF=FC,根据四边相等的四边形是菱形,所以四边形BECF是菱形;
(2)由菱形的性质知,对角线平分一组对角,即当∠ABC=45°时,∠EBF=90°,有菱形为正方形,根据直角三角形中两个角锐角互余得,∠A=45度.
解答 解:(1)四边形BECF是菱形.
∵EF垂直平分BC,
∴BF=FC,BE=EC,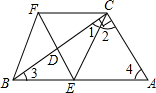
∴∠3=∠1,
∵∠ACB=90°,
∴∠3+∠4=90°,∠1+∠2=90°,
∴∠2=∠4,
∴EC=AE,
∴BE=AE,
∵CF=AE,
∴BE=EC=CF=BF,
∴四边形BECF是菱形.
(2)当∠A=45°时,菱形BECF是正方形.
证明:∵∠A=45°,∠ACB=90°,
∴∠1=45°,
∴∠EBF=2∠A=90°,
∴菱形BECF是正方形.
点评 本题考查菱形的判定和性质以及正方形的判定,有一定难度,解题关键是熟练掌握菱形的判定方法及性质并灵活运用.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
10.如果|a|=3,|b|=7,那么|a+b|=( )
| A. | 10 | B. | 4 | C. | 10或4 | D. | -10或-4 |
7.在四边形ABCD中,AB=BC=CD=DA,如果添加一个条件,即可推出该四边形是正方形,那么这个条件可以是( )
| A. | AC⊥BD | B. | AB∥CD | C. | ∠A=90° | D. | ∠A=∠C |
11.-9的相反数为( )
| A. | 9 | B. | -9 | C. | -6 | D. | 6 |
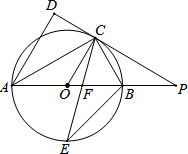 如图,AB是⊙O的直径,点C是⊙O上一点,AD与过点C的切线垂直,垂足为点D,直线DC与AB的延长线相交于点P,弦CE平分∠ACB,交AB于点F,连接BE.
如图,AB是⊙O的直径,点C是⊙O上一点,AD与过点C的切线垂直,垂足为点D,直线DC与AB的延长线相交于点P,弦CE平分∠ACB,交AB于点F,连接BE.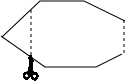 如图,一个多边形纸片按图示的剪法剪去一个内角后,得到一个内角和为2340°的新多边形,则原多边形的边数为14.
如图,一个多边形纸片按图示的剪法剪去一个内角后,得到一个内角和为2340°的新多边形,则原多边形的边数为14.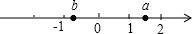 实数a,b在数轴上的位置如图所示,则化简$\sqrt{(a-b)^{2}}$-$\sqrt{(1-a)^{2}}$-$\sqrt{{b}^{2}}$结果是( )
实数a,b在数轴上的位置如图所示,则化简$\sqrt{(a-b)^{2}}$-$\sqrt{(1-a)^{2}}$-$\sqrt{{b}^{2}}$结果是( )