题目内容
16.解方程组:(1)$\left\{\begin{array}{l}{2x-3y+13=0}\\{9x+6y-8=0}\end{array}\right.$
(2)$\left\{\begin{array}{l}{\frac{x+y}{2}=6-\frac{x-y}{3}}\\{3(x+y)+5(x-y)=2}\end{array}\right.$.
分析 (1)方程组整理后,利用加减消元法求出解即可;
(2)方程组整理后,利用加减消元法求出解即可.
解答 解:(1)方程组整理得:$\left\{\begin{array}{l}{2x-3y=-13①}\\{9x+6y=8②}\end{array}\right.$,
①×2+②得:13x=-18,即x=-$\frac{18}{13}$,
把x=-$\frac{18}{13}$代入①得:y=$\frac{133}{39}$,
则方程组的解为$\left\{\begin{array}{l}{x=-\frac{18}{13}}\\{y=\frac{133}{39}}\end{array}\right.$;
(2)方程组整理得:$\left\{\begin{array}{l}{5x+y=36①}\\{4x-y=1②}\end{array}\right.$,
①+②得:9x=37,即x=$\frac{37}{9}$,
把x=$\frac{37}{9}$代入②得:y=$\frac{139}{9}$,
则方程组的解为$\left\{\begin{array}{l}{x=\frac{37}{9}}\\{y=\frac{139}{9}}\end{array}\right.$.
点评 此题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.

练习册系列答案
相关题目
 探照灯、汽车灯等很多灯具都与平行线有关,如图所示是一探照灯碗的剖面,从位于O点的灯泡发出的两束光线OB,OC,经灯碗反射以后平行射出,其中∠ABO=α,∠BOC=β,则∠DCO的度数是β-α.
探照灯、汽车灯等很多灯具都与平行线有关,如图所示是一探照灯碗的剖面,从位于O点的灯泡发出的两束光线OB,OC,经灯碗反射以后平行射出,其中∠ABO=α,∠BOC=β,则∠DCO的度数是β-α.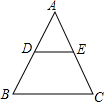 如图,D、E分别是△ABC的边AB、AC上的点,且AD=DB,AE=EC,若DE=4,则BC长为( )
如图,D、E分别是△ABC的边AB、AC上的点,且AD=DB,AE=EC,若DE=4,则BC长为( )