题目内容
1.观察下列一组等式的规律,然后解答后面的问题.($\sqrt{2}$+1)($\sqrt{2}$-1)=1;
($\sqrt{3}$+$\sqrt{2}$)($\sqrt{3}$-$\sqrt{2}$)=1;
($\sqrt{4}$+$\sqrt{3}$)($\sqrt{4}$-$\sqrt{3}$)=1;
($\sqrt{5}$+$\sqrt{4}$)($\sqrt{5}$-$\sqrt{4}$)=1;
…
(1)计算:$\frac{1}{\sqrt{2}+1}$+$\frac{1}{\sqrt{3}+\sqrt{2}}$+$\frac{1}{\sqrt{4}+\sqrt{3}}$+…+$\frac{1}{\sqrt{2015}+\sqrt{2014}}$;
(2)比较$\sqrt{11}$-$\sqrt{10}$与$\sqrt{12}$-$\sqrt{11}$的大小.
分析 (1)先进行分母有理化,再利用规律求解即可,
(2)先化简,再比较即可.
解答 解:(1)$\frac{1}{\sqrt{2}+1}$+$\frac{1}{\sqrt{3}+\sqrt{2}}$+$\frac{1}{\sqrt{4}+\sqrt{3}}$+…+$\frac{1}{\sqrt{2015}+\sqrt{2014}}$
=$\sqrt{2}$-1+$\sqrt{3}$-$\sqrt{2}$+…$\sqrt{2015}$-$\sqrt{2014}$,
=$\sqrt{2015}$-1;
(2)$\sqrt{11}$-$\sqrt{10}$=$\frac{1}{\sqrt{11}+\sqrt{10}}$,$\sqrt{12}$-$\sqrt{11}$=$\frac{1}{\sqrt{12}+\sqrt{11}}$,
∵$\sqrt{11}$+$\sqrt{10}$<$\sqrt{12}$+$\sqrt{11}$,
∴$\frac{1}{\sqrt{11}+\sqrt{10}}$>$\frac{1}{\sqrt{12}+\sqrt{11}}$,
∴$\sqrt{11}$-$\sqrt{10}$>$\sqrt{12}$-$\sqrt{11}$.
点评 本题主要考查了分母有理化,解题的关键是正确的化简.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
11.“中国汉字听写大会”是由中央电视台和国家语言文字工作委员会联合主办的节目,希望通过节目的播出,能吸引更多的人关注对汉字文化的学习.某校也开展了一次“汉字听写”比赛,每位参赛学生听写40个汉字.比赛结束后随机抽取部分学生的听写结果,按听写正确的汉字个数x绘制成了以下不完整的统计图.
根据以上信息回答下列问题:
(1)本次共随机抽取了50名学生进行调查,听写正确的汉字个数x在21≤x<31范围的人数最多;
(2)补全频数分布直方图;
(3)各组的组中值如下表所示.若用各组的组中值代表各组每位学生听写正确的汉字个数,求被调查学生听写正确的汉字个数的平均数;
(4)该校共有1350名学生,如果听写正确的汉字个数不少于21个定为良好,请你估计该校本次“汉字听写”比赛达到良好的学生人数.

根据以上信息回答下列问题:
(1)本次共随机抽取了50名学生进行调查,听写正确的汉字个数x在21≤x<31范围的人数最多;
(2)补全频数分布直方图;
(3)各组的组中值如下表所示.若用各组的组中值代表各组每位学生听写正确的汉字个数,求被调查学生听写正确的汉字个数的平均数;
| 听写正确的汉字个数x | 组中值 |
| 1≤x<11 | 6 |
| 11≤x<21 | 16 |
| 21≤x<31 | 26 |
| 31≤x<41 | 36 |
2.某学校的复印任务原来由甲复印社承接,其收费y(元)与复印页数x的关系如下表:
(1)求y与x的函数关系式.
(2)现在乙复印社表示:若学校先按每月付给200元的承包费,则可按每页0.15元收费,求乙复印社每月收费y(元)与复印页数x的函数关系式.
(3)如果学校每月复印页数在1200左右,应选择哪个复印社?为什么?
| x | 100 | 200 | 400 | 1000 | … |
| y(元) | 40 | 80 | 160 | 400 | … |
(2)现在乙复印社表示:若学校先按每月付给200元的承包费,则可按每页0.15元收费,求乙复印社每月收费y(元)与复印页数x的函数关系式.
(3)如果学校每月复印页数在1200左右,应选择哪个复印社?为什么?
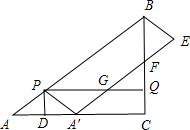 如图,在Rt△ABC中,∠ACB=90°,AC=8cm,AB=10cm.点P从点A出发,以5cm/s的速度从点A运动到终点B;同时,点Q从点C出发,以3cm/s的速度从点C运动到终点B,连结PQ;过点P作PD⊥AC交AC于点D,将△APD沿PD翻折得到△A′PD,以A′P和PB为邻边作?A′PBE,A′E交射线BC于点F,交射线PQ于点G.设?A′PBE与四边形PDCQ重叠部分图形的面积为Scm2,点P的运动时间为ts.
如图,在Rt△ABC中,∠ACB=90°,AC=8cm,AB=10cm.点P从点A出发,以5cm/s的速度从点A运动到终点B;同时,点Q从点C出发,以3cm/s的速度从点C运动到终点B,连结PQ;过点P作PD⊥AC交AC于点D,将△APD沿PD翻折得到△A′PD,以A′P和PB为邻边作?A′PBE,A′E交射线BC于点F,交射线PQ于点G.设?A′PBE与四边形PDCQ重叠部分图形的面积为Scm2,点P的运动时间为ts.