题目内容
7.(1)设a、b同时满足(a-2b)2+|b+1|=b+1和|a+b-3|=0,那么ab=2;(2)已知(a+b)2+|b+5|=b+5,且|2a-b-1|=0,那么ab=-1.
分析 (1)根据非负数的性质列式$\left\{\begin{array}{l}{a-2b=0}\\{a+b-3=0}\end{array}\right.$求出a、b的值,然后代入代数式进行计算即可得解;
(2)根据非负数的性质列式$\left\{\begin{array}{l}{a+b=0}\\{2a-b-1=0}\end{array}\right.$求出a、b的值,然后代入代数式进行计算即可得解.
解答 解:(1)依题意有$\left\{\begin{array}{l}{a-2b=0}\\{a+b-3=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=2}\\{b=1}\end{array}\right.$,
则ab=2×1=2.
故答案为:2;
(2)依题意有$\left\{\begin{array}{l}{a+b=0}\\{2a-b-1=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=\frac{1}{3}}\\{b=-\frac{1}{3}}\end{array}\right.$,
则ab=$\frac{1}{3}$×(-$\frac{1}{3}$)=-1.
故答案为:-1.
点评 本题考查了非负数的性质:几个非负数的和为0时,这几个非负数都为0.

练习册系列答案
相关题目
17. 如图,在△ABC中,D、E分别是边AB、AC的中点,若BC=6,则DE的长为( )
如图,在△ABC中,D、E分别是边AB、AC的中点,若BC=6,则DE的长为( )
 如图,在△ABC中,D、E分别是边AB、AC的中点,若BC=6,则DE的长为( )
如图,在△ABC中,D、E分别是边AB、AC的中点,若BC=6,则DE的长为( )| A. | 2 | B. | 3 | C. | 4 | D. | 6 |
 在平面坐标系中,正方形ABCD的位置如图,点A的坐标为(1,0),点D的坐标为(0,2),延长CB交于x轴于点A1,作正方形A1B1C1C,延长C1B1交x轴于点A2,作正方形A2B2C2C1,…按这样的规律进行下去,第2016个正方形A2015B2015C2015C2014的面积为5×($\frac{9}{4}$)2015.
在平面坐标系中,正方形ABCD的位置如图,点A的坐标为(1,0),点D的坐标为(0,2),延长CB交于x轴于点A1,作正方形A1B1C1C,延长C1B1交x轴于点A2,作正方形A2B2C2C1,…按这样的规律进行下去,第2016个正方形A2015B2015C2015C2014的面积为5×($\frac{9}{4}$)2015.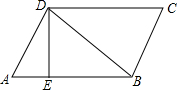 如图,?ABCD的周长为52cm,AB边的垂直平分线经过点D,垂足为E,?ABCD的周长比△ABD的周长多10cm.∠BDE=35°.
如图,?ABCD的周长为52cm,AB边的垂直平分线经过点D,垂足为E,?ABCD的周长比△ABD的周长多10cm.∠BDE=35°.