题目内容
11．解不等式：|x-1|+|x-3|＞4．分析 分成x＜1或1≤x＜3以及x≥3三种情况进行讨论，去掉绝对值符号求解即可．
解答 解：当x＜1时，原式即1-x+3-x＞4，
解得：x＜0；
当1≤x＜3时，原式即x-1+（3-x）＞4，
不等式无解；
当x≥3时，原式即x-1+x-3＞4，
解得：x＞4．
总之x的范围是：x＜0或x＞4．
点评 本题考查了含有绝对值的不等式的解法，正确进行讨论，去掉绝对值符号是关键．
练习册系列答案
相关题目
题目内容
11．解不等式：|x-1|+|x-3|＞4．分析 分成x＜1或1≤x＜3以及x≥3三种情况进行讨论，去掉绝对值符号求解即可．
解答 解：当x＜1时，原式即1-x+3-x＞4，
解得：x＜0；
当1≤x＜3时，原式即x-1+（3-x）＞4，
不等式无解；
当x≥3时，原式即x-1+x-3＞4，
解得：x＞4．
总之x的范围是：x＜0或x＞4．
点评 本题考查了含有绝对值的不等式的解法，正确进行讨论，去掉绝对值符号是关键．
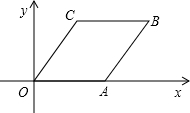如图，平行四边形OABC的顶点O，A，C的坐标分别是（0，0），（3，0），（1，2），则顶点B的坐标是（4，2）．
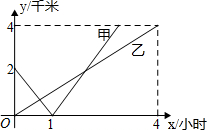已知A、B、C是同一条笔直公路上的三个不同的车站，甲、乙两人分别从A、B车站同时出发，匀速直线运动到C站，到达C站就停下来，甲、乙两人与B站的距离y（千米）与时间x（小时）之间的函数关系的图象如图，当甲出发7小时，甲、乙两人相距5千米．
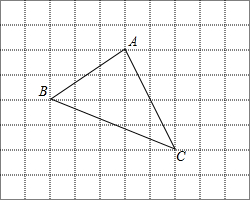如图是一个被抹去x轴、y轴及原点O的网格图，网格中每个小正方形的边长均为1个单位长度，三角形ABC的各顶点都在网格的格点上，若记点A的坐标为（-1，3），点C的坐标为（1，-1）．