题目内容
17.若一个正多边形的一个内角与它相邻的一个外角的差是100°,则这个多边形的边数是9.分析 设这个正多边形的每个外角的度数为x,则每个内角为x+100°,利用多边形的外角与相邻的内角互补得到x+x+100°=180°,解方程得x=40°,然后根据n边的外角和为360°即可得到这个多边形的边数.
解答 解:设这个正多边形的每个外角的度数为x,则每个内角为x+100°,
∴x+x+100°=180°,
∴x=40°,
∴这个多边形的边数=$\frac{360°}{40°}$=9.
故答案为:9
点评 本题考查了多边形的内角和和外角和定理:n边形的内角和为(n-2)×180°;n边的外角和为360°.

练习册系列答案
相关题目
5.在平面直角坐标系xOy中,已知点P在x轴下方,在y轴右侧,且点P到x轴的距离为3,到y轴的距离为4,则点P的坐标为( )
| A. | (-3,4) | B. | (-4,3) | C. | (3,-4) | D. | (4,-3) |
2.某学校的复印任务原来由甲复印社承接,其收费y(元)与复印页数x的关系如下表:
(1)求y与x的函数关系式.
(2)现在乙复印社表示:若学校先按每月付给200元的承包费,则可按每页0.15元收费,求乙复印社每月收费y(元)与复印页数x的函数关系式.
(3)如果学校每月复印页数在1200左右,应选择哪个复印社?为什么?
| x | 100 | 200 | 400 | 1000 | … |
| y(元) | 40 | 80 | 160 | 400 | … |
(2)现在乙复印社表示:若学校先按每月付给200元的承包费,则可按每页0.15元收费,求乙复印社每月收费y(元)与复印页数x的函数关系式.
(3)如果学校每月复印页数在1200左右,应选择哪个复印社?为什么?
6.老师在计算学期总平均分的时候按照如下标准:作业占10%,测验占30%,期中考试占25%,期末考试占35%.小丽和小明的成绩如下表所示,求小丽和小明的总平均分.
| 学生 | 作业 | 测验 | 期中考试 | 期末考试 |
| 小丽 | 80 | 75 | 71 | 88 |
| 小明 | 76 | 80 | 68 | 90 |
7.下列各数中,是方程x2-2x=3的根的是( )
| A. | 1 | B. | 0 | C. | 3 | D. | -3 |
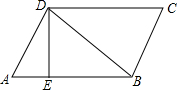 如图,?ABCD的周长为52cm,AB边的垂直平分线经过点D,垂足为E,?ABCD的周长比△ABD的周长多10cm.∠BDE=35°.
如图,?ABCD的周长为52cm,AB边的垂直平分线经过点D,垂足为E,?ABCD的周长比△ABD的周长多10cm.∠BDE=35°.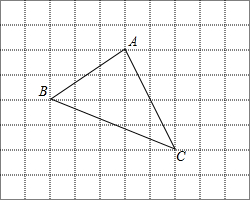 如图是一个被抹去x轴、y轴及原点O的网格图,网格中每个小正方形的边长均为1个单位长度,三角形ABC的各顶点都在网格的格点上,若记点A的坐标为(-1,3),点C的坐标为(1,-1).
如图是一个被抹去x轴、y轴及原点O的网格图,网格中每个小正方形的边长均为1个单位长度,三角形ABC的各顶点都在网格的格点上,若记点A的坐标为(-1,3),点C的坐标为(1,-1).