题目内容
8.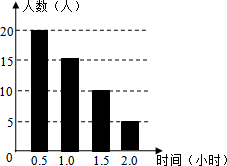 某校为了解学生课外阅读情况,随机调查了50名学生各自平均每天的课外阅读时间,并绘制成条形图,据此可以估计出该校所有学生平均每人每天的课外阅读时间为1小时.
某校为了解学生课外阅读情况,随机调查了50名学生各自平均每天的课外阅读时间,并绘制成条形图,据此可以估计出该校所有学生平均每人每天的课外阅读时间为1小时.
分析 根据加权平均数的求解方法列式计算即可得解.
解答 解:$\frac{1}{50}$×(20×0.5+15×1+10×1.5+5×2),
=$\frac{1}{50}$×(10+15+15+10),
=$\frac{1}{50}$×50,
=1(小时).
故答案为:1小时.
点评 本题考查的是条形统计图的综合运用,加权平均数的求法.读懂统计图,从统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据.

练习册系列答案
相关题目
19.要使分式$\frac{x-3}{{{x^2}+6x+9}}$有意义,那么x的取值范围是( )
| A. | x≠3 | B. | x≠3且x≠-3 | C. | x≠0且x≠-3 | D. | x≠-3 |
3.若A(1,y1),B(2,y2)两点都在反比例函数y=$\frac{1}{x}$的图象上,则y1与y2的大小关系是( )
| A. | y1<y2 | B. | y1=y2 | C. | y1>y2 | D. | 无法确定 |
19.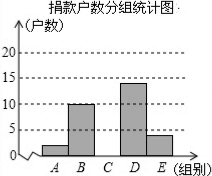 为了让更多的失学儿童重返校园,某社区组织“献爱心手拉手”捐款活动,对社区部分捐款户数进行调查和分组统计后,将数据整理成如图所示的统计图(图中信息不完整).
为了让更多的失学儿童重返校园,某社区组织“献爱心手拉手”捐款活动,对社区部分捐款户数进行调查和分组统计后,将数据整理成如图所示的统计图(图中信息不完整).
捐款户数分组统计表
请结合以上信息解答下列问题.
(1)a=0.28,本次调查样本的容量是50;
(2)先求出C组的户数为20户,再补全“捐款户数分组统计图”;
(3)直接写出捐款额的中位数落在C组.
 为了让更多的失学儿童重返校园,某社区组织“献爱心手拉手”捐款活动,对社区部分捐款户数进行调查和分组统计后,将数据整理成如图所示的统计图(图中信息不完整).
为了让更多的失学儿童重返校园,某社区组织“献爱心手拉手”捐款活动,对社区部分捐款户数进行调查和分组统计后,将数据整理成如图所示的统计图(图中信息不完整).捐款户数分组统计表
| 组别 | 捐款额(x)元 | 户数 | 频率 |
| A | 1≤x<100 | 2 | 0.04 |
| B | 100≤x<200 | 10 | 0.2 |
| C | 200≤x<300 | 0.4 | |
| D | 300≤x<400 | 14 | a |
| E | x≥400 | 4 | 0.08 |
(1)a=0.28,本次调查样本的容量是50;
(2)先求出C组的户数为20户,再补全“捐款户数分组统计图”;
(3)直接写出捐款额的中位数落在C组.
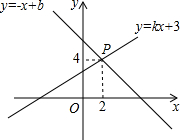 如图,已知一次函数y=kx+3和y=-x+b的图象交于点P(2,4),则关于x的方程kx+3=-x+b的解是x=2.
如图,已知一次函数y=kx+3和y=-x+b的图象交于点P(2,4),则关于x的方程kx+3=-x+b的解是x=2. 如图,二次函数$y=\frac{1}{2}{(x-3)^2}-1$的图象与x轴交于A,B两点(点A在点B左侧),与y轴交于点C,顶点为D.
如图,二次函数$y=\frac{1}{2}{(x-3)^2}-1$的图象与x轴交于A,B两点(点A在点B左侧),与y轴交于点C,顶点为D.