题目内容
18.有三张正面分别标有数字:-1,1,2的卡片,它们除数字不同外其余全部相同,现将它们背面朝上,洗匀后从中抽出一张记下数字,放回洗匀后再从中随机抽出一张记下数字.(1)请用列表或画树形图的方法(只选其中一种),表示两次抽出卡片上的数字的所有结果;
(2)若第一次抽出的数字为x,第二次抽出的数字为y,求点(x,y)落在双曲线y=$\frac{2}{x}$上的概率.
分析 (1)画树状图展示所有9种等可能的结果数;
(2)根据反比例函数图象上点的坐标特征找出点(x,y)落在双曲线y=$\frac{2}{x}$上的结果数,然后根据概率公式求解.
解答 解:(1)画树状图为:
共有9种等可能的结果数;
(2)点(x,y)落在双曲线y=$\frac{2}{x}$上的结果数为2,
所以点(x,y)落在双曲线y=$\frac{2}{x}$上的概率=$\frac{2}{9}$.
点评 本题考查了列表法与树状图法:通过列表法或树状图法展示所有等可能的结果求出n,再从中选出符合事件A或B的结果数目m,然后根据概率公式求出事件A或B的概率.也考查了反比例函数函数图象上点的坐标特征.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
8.下列图形是中心对称而不是轴对称的是( )
| A. |  | B. |  | C. |  | D. |  |
9.如图所示,长为2宽为1的矩形和边长为3的正方形在同一水平线上,矩形沿该水平线从左向右匀速穿过正方形;设穿过的时间为t,正方形除去矩形面积为S(阴影部分),则S与t的大致图象为( )
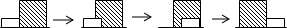
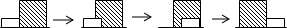
| A. | 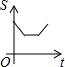 | B. | 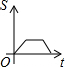 | C. | 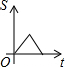 | D. | 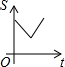 |
6.下列命题:
①同旁内角互补;
②如果直线a,b,c满足a∥b,b∥c,那么a∥c;
③1的平方根和立方根都是1;
④若x>y,则a2x>a2y;
⑤如果A(a,b)在x轴上,那么B(b,a)在y轴上,
其中,假命题的个数有( )
①同旁内角互补;
②如果直线a,b,c满足a∥b,b∥c,那么a∥c;
③1的平方根和立方根都是1;
④若x>y,则a2x>a2y;
⑤如果A(a,b)在x轴上,那么B(b,a)在y轴上,
其中,假命题的个数有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
13.已知菱形ABCD的对角线AC,BD的长分别为6和8,则该菱形面积是( )
| A. | 14 | B. | 24 | C. | 30 | D. | 48 |
3.不等式x+3<2的解集是( )
| A. | x<1 | B. | x<-1 | C. | x>1 | D. | x>-1 |
10.如图图形中,既是轴对称图形又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
7.阅读对人成长的影响是巨大的,一本好书往往能改变人的一生,每年的4月23日被联合国教科文组织确定为“世界读书日”.某校本学年开展了读书活动,在这次活动中,八年级(1)班40名学生读书册数的情况如表:
根据表中的数据,求:
(1)该班学生读书册数的平均数;
(2)该班学生读书册数的中位数.
| 读书册数 | 4 | 5 | 6 | 7 | 8 |
| 人数(人) | 6 | 4 | 10 | 12 | 8 |
(1)该班学生读书册数的平均数;
(2)该班学生读书册数的中位数.
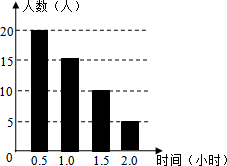 某校为了解学生课外阅读情况,随机调查了50名学生各自平均每天的课外阅读时间,并绘制成条形图,据此可以估计出该校所有学生平均每人每天的课外阅读时间为1小时.
某校为了解学生课外阅读情况,随机调查了50名学生各自平均每天的课外阅读时间,并绘制成条形图,据此可以估计出该校所有学生平均每人每天的课外阅读时间为1小时.