题目内容
12.(1)已知:如图,在正方形ABCD中,点E在边CD上,AQ⊥BE于点Q,DP⊥AQ于点P,求证:AP=BQ.(2)如图,已知AB是⊙O的直径,AC是⊙O的弦,过点C的切线交AB的延长线于点D且∠A=∠D.求∠D的度数.
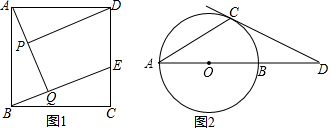
分析 (1)由正方形的性质知AD=BA、∠BAD=90°,由AQ⊥BE、DP⊥AQ知∠BAQ=∠ADP、∠AQB=∠DPA=90°,即可证△AQB≌△DPA得AP=BQ;
(2)由切线的性质知∠OCD=90°即∠COB+∠D=90°,由圆周角定理知∠COB=2∠A,结合∠A=∠D可得答案.
解答 解:(1)∵四边形ABCD为正方形,
∴AD=BA,∠BAD=90°,即∠BAQ+∠DAP=90°,
∵DP⊥AQ,
∴∠ADP+∠DAP=90°,
∴∠BAQ=∠ADP,
∵AQ⊥BE于点Q,DP⊥AQ于点P,
∴∠AQB=∠DPA=90°,
在△AQB和△DPA中,
∵$\left\{\begin{array}{l}{∠BAQ=∠ADP}\\{∠AQB=∠DPA}\\{AB=DA}\end{array}\right.$,
∴△AQB≌△DPA(AAS),
∴AP=BQ;
(2)如图,连接OC,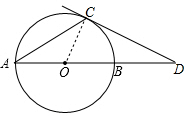
∵CD是⊙O 的切线,
∴OC⊥CD,
∴∠OCD=90°,
∴∠COB+∠D=90°,
由圆周角定理得∠COB=2∠A,
∵∠A=∠D,
∴2∠A+∠A=90°,
∴∠A=30°,
∴∠D=30°.
点评 本题主要考查正方形的性质、切线的性质、圆周角定理及全等三角形的判定与性质,熟练掌握正方形的性质、切线的性质是解题的关键.

练习册系列答案
相关题目
20.某公司需要从甲、乙两个仓库向A、B两地分别运送100t和50t的物资.已知该物资在甲仓库有80t,乙仓库有70t.从甲、乙两个仓库运送物资到A、B两地的运费如下表:
(1)设从甲仓库运送到A地的物资为xt,求运送的总运费y(单位:元)与x(单位:t)之间的函数解析式,并写出x的取值范围.
(2)请你设计出运费最低的运送方案,并求出最低运费.
| 目的地 | 运费/(元/t) | |
| 甲仓库 | 乙仓库 | |
| A地 | 140 | 200 |
| B地 | 100 | 80 |
(2)请你设计出运费最低的运送方案,并求出最低运费.
1.若a+b=3,则代数式($\frac{{b}^{2}}{a}$-a)÷$\frac{a-b}{a}$的值为( )
| A. | 3 | B. | -3 | C. | $\frac{1}{3}$ | D. | -$\frac{1}{3}$ |
2.计算:(-1)2017的值是( )
| A. | 1 | B. | -1 | C. | 2017 | D. | -2017 |
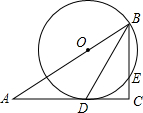 如图,在Rt△ABC中,C=90°,BD是角平分线,点O在AB上,以点O为圆心,OB为半径的圆经过点D,交BC于点E.
如图,在Rt△ABC中,C=90°,BD是角平分线,点O在AB上,以点O为圆心,OB为半径的圆经过点D,交BC于点E.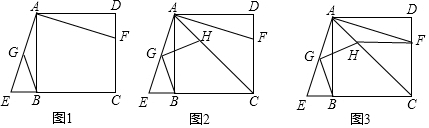
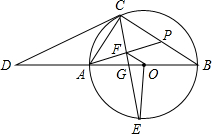 如图,AB为⊙O的直径,CD切⊙O于点C,与BA的延长线交于点D,OE⊥AB交⊙O于点E,连接CA、CE、CB,CE交AB于点G,过点A作AF⊥CE于点F,延长AF交BC于点P.
如图,AB为⊙O的直径,CD切⊙O于点C,与BA的延长线交于点D,OE⊥AB交⊙O于点E,连接CA、CE、CB,CE交AB于点G,过点A作AF⊥CE于点F,延长AF交BC于点P.