题目内容
10.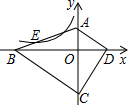 如图,四边形ABCD的顶点都在坐标轴上,若AD∥BC,△ACD与△BCD的面积分别为10和20,若双曲线y=$\frac{k}{x}$恰好经过边AB的四等分点E(BE<AE),则k的值为-$\frac{5}{2}$.
如图,四边形ABCD的顶点都在坐标轴上,若AD∥BC,△ACD与△BCD的面积分别为10和20,若双曲线y=$\frac{k}{x}$恰好经过边AB的四等分点E(BE<AE),则k的值为-$\frac{5}{2}$.
分析 由AD∥BC,可得出S△BCD=S△BCA、S△ACD=S△ABD,根据△ACD与△BCD的面积分别为10和20结合同底三角形面积的性质,即可得出AO:OC=DO:OB=1:2,进而可得出S△AOB=$\frac{20}{3}$,再根据反比例函数系数k的几何意义以及相似三角形的性质得出|k|=$\frac{6}{16}$×$\frac{20}{3}$=$\frac{5}{2}$,解之即可得出结论.
解答 解:∵AD∥BC,
∴S△BCD=S△BCA,S△ACD=S△ABD.
∵△ACD与△BCD的面积分别为10和20,
∴△ABD和△BCD面积比为1:2,
∴根据同底得:AO:OC=DO:OB=1:2,
∴S△AOB=$\frac{2}{2+1}$S△ABD=$\frac{2}{3}$×10=$\frac{20}{3}$.
∵双曲线y=$\frac{k}{x}$恰好经过边AB的四等分点E(BE<AE),
∴$\frac{1}{16}$S△AOB+|k|+$\frac{9}{16}$S△AOB=S△AOB,
∴|k|=$\frac{6}{16}$S△AOB=$\frac{6}{16}$×$\frac{20}{3}$=$\frac{5}{2}$,
∵双曲线经过第二象限,k<0,
∴k=-$\frac{5}{2}$.
故答案为-$\frac{5}{2}$.
点评 本题考查了反比例函数系数k的几何意义、三角形的面积、平行线的性质、相似三角形的性质,根据平行线的性质结合三角形面积间的关系得出S△AOB=$\frac{20}{3}$是解题的关键.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
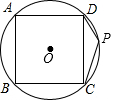 如图,正方形ABCD的四个顶点分别在⊙O上,点P在$\widehat{CD}$上不同于点C的任意一点,则∠DPC的度数是135度.
如图,正方形ABCD的四个顶点分别在⊙O上,点P在$\widehat{CD}$上不同于点C的任意一点,则∠DPC的度数是135度.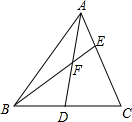 已知如图,F为AD的中点,$\frac{AE}{EC}$=$\frac{1}{2}$,求$\frac{BD}{CD}$和$\frac{BF}{FE}$.
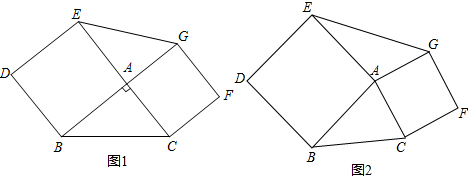
已知如图,F为AD的中点,$\frac{AE}{EC}$=$\frac{1}{2}$,求$\frac{BD}{CD}$和$\frac{BF}{FE}$.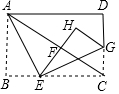 如图,将矩形纸片ABCD沿AE折叠,使点B落在对角线AC上的点F处,再沿EG折叠,使点C落在矩形内的点H处,且E、F、H在同一直线上,若AB=6,BC=8,则CG的长是$\frac{5}{2}$.
如图,将矩形纸片ABCD沿AE折叠,使点B落在对角线AC上的点F处,再沿EG折叠,使点C落在矩形内的点H处,且E、F、H在同一直线上,若AB=6,BC=8,则CG的长是$\frac{5}{2}$.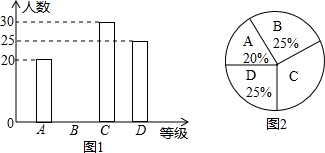
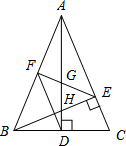 如图,在△ABC中,AB=AC,AD和BE是高,∠ABE=45°,点F是AB的中点,AD与FE、BE分别交于点G、H.有下列结论:①FD=FE;②AH=2CD;③BC•AD=$\sqrt{2}$AE2;④S△ABC=4S△ADF.其中正确结论的序号是①②③④.(把你认为正确结论的序号都填上).
如图,在△ABC中,AB=AC,AD和BE是高,∠ABE=45°,点F是AB的中点,AD与FE、BE分别交于点G、H.有下列结论:①FD=FE;②AH=2CD;③BC•AD=$\sqrt{2}$AE2;④S△ABC=4S△ADF.其中正确结论的序号是①②③④.(把你认为正确结论的序号都填上).