题目内容
19.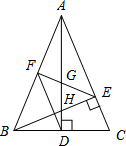 如图,在△ABC中,AB=AC,AD和BE是高,∠ABE=45°,点F是AB的中点,AD与FE、BE分别交于点G、H.有下列结论:①FD=FE;②AH=2CD;③BC•AD=$\sqrt{2}$AE2;④S△ABC=4S△ADF.其中正确结论的序号是①②③④.(把你认为正确结论的序号都填上).
如图,在△ABC中,AB=AC,AD和BE是高,∠ABE=45°,点F是AB的中点,AD与FE、BE分别交于点G、H.有下列结论:①FD=FE;②AH=2CD;③BC•AD=$\sqrt{2}$AE2;④S△ABC=4S△ADF.其中正确结论的序号是①②③④.(把你认为正确结论的序号都填上).
分析 由直角三角形斜边上的中线性质得出FD=$\frac{1}{2}$AB,证明△ABE是等腰直角三角形,得出AE=BE,证出FE=$\frac{1}{2}$AB,延长FD=FE,①正确;
证出∠ABC=∠C,得出AB=AC,由等腰三角形的性质得出BC=2CD,∠BAD=∠CAD=∠CBE,由ASA证明△AEH≌△BEC,得出AH=BC=2CD,②正确;
证明△ABD~△BCE,得出$\frac{BE}{AD}$=$\frac{CB}{AB}$,即BC•AD=AB•BE,再由等腰直角三角形的性质和三角形的面积得出BC•AD=$\sqrt{2}$AE2;③正确;
由F是AB的中点,BD=CD,得出S△ABC=2S△ABD=4S△ADF.④正确;即可得出结论.
解答 解:∵在△ABC中,AD和BE是高,
∴∠ADB=∠AEB=∠CEB=90°,
∵点F是AB的中点,
∴FD=$\frac{1}{2}$AB,
∵∠ABE=45°,
∴△ABE是等腰直角三角形,
∴AE=BE,
∵点F是AB的中点,
∴FE=$\frac{1}{2}$AB,
∴FD=FE,①正确;
∵∠CBE=∠BAD,∠CBE+∠C=90°,∠BAD+∠ABC=90°,
∴∠ABC=∠C,
∴AB=AC,
∵AD⊥BC,
∴BC=2CD,∠BAD=∠CAD=∠CBE,
在△AEH和△BEC中$\left\{\begin{array}{l}{∠AEH=∠CEB}\\{AE=BE}\\{∠EAH=∠CBE}\end{array}\right.$,
∴△AEH≌△BEC(ASA),
∴AH=BC=2CD,②正确;
∵∠BAD=∠CBE,∠ADB=∠CEB,
∴△ABD~△BCE,
∴$\frac{BE}{AD}$=$\frac{CB}{AB}$,即BC•AD=AB•BE,
∵$\sqrt{2}$AE2=AB•AE=AB•BE,BC•AD=AC•BE=AB•BE,
∴BC•AD=$\sqrt{2}$AE2;③正确;
∵F是AB的中点,BD=CD,∴
S△ABC=2S△ABD=4S△ADF.④正确;
故答案为:①②③④.
点评 本题考查了相似三角形的判定与性质、全等三角形的判定与性质、直角三角形斜边上的中线性质、等腰三角形的判定与性质;本题综合性强,有一定难度,证明三角形相似和三角形全等是解决问题的关键.

 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案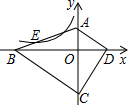 如图,四边形ABCD的顶点都在坐标轴上,若AD∥BC,△ACD与△BCD的面积分别为10和20,若双曲线y=$\frac{k}{x}$恰好经过边AB的四等分点E(BE<AE),则k的值为-$\frac{5}{2}$.
如图,四边形ABCD的顶点都在坐标轴上,若AD∥BC,△ACD与△BCD的面积分别为10和20,若双曲线y=$\frac{k}{x}$恰好经过边AB的四等分点E(BE<AE),则k的值为-$\frac{5}{2}$.
 如图,为了测量山顶铁塔AE的高,小明在25m高的楼CD底部D测得塔顶A的仰角为45°,在楼顶C测得塔顶A的仰角36°52′.已知山高BE为58m,楼的底部D与山脚在同一水平线上,求该铁塔的高AE.(参考数据:sin36°52′≈0.60,tan36°52′≈0.75)
如图,为了测量山顶铁塔AE的高,小明在25m高的楼CD底部D测得塔顶A的仰角为45°,在楼顶C测得塔顶A的仰角36°52′.已知山高BE为58m,楼的底部D与山脚在同一水平线上,求该铁塔的高AE.(参考数据:sin36°52′≈0.60,tan36°52′≈0.75)