题目内容
7.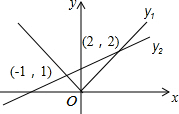 函数y1=|x|,y2=$\frac{1}{3}$x+$\frac{4}{3}$.当y1<y2时,x的范围是( )
函数y1=|x|,y2=$\frac{1}{3}$x+$\frac{4}{3}$.当y1<y2时,x的范围是( )| A. | x<-1 | B. | -1<x<2 | C. | x<-1或x>2 | D. | x>2 |
分析 由图象可知:函数y1=|x|与y2=$\frac{1}{3}$x+$\frac{4}{3}$的图象交于点(-1,1),(2,2),y1的图象落在y2图象下方的部分对应的x的取值范围即为所求.
解答 解:由图象可知:当-1<x<2时,y1的图象落在y2图象的下方,即y1<y2,
所以当y1<y2时,x的范围是-1<x<2.
故选B.
点评 此题主要考查了一次函数与一元一次不等式的关系:从函数的角度看,就是寻求使一次函数y=kx+b的值大于(或小于)0的自变量x的取值范围;从函数图象的角度看,就是确定直线y=kx+b在x轴上(或下)方部分所有的点的横坐标所构成的集合.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
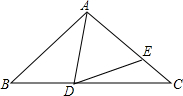 如图,在等腰三角形ABC中,AB=AC,等边三角形ADE的顶点D,E分别落在AC,AC上,若AD=BD,求∠EDC的度数.
如图,在等腰三角形ABC中,AB=AC,等边三角形ADE的顶点D,E分别落在AC,AC上,若AD=BD,求∠EDC的度数.