题目内容
16.一个口袋中有红球,白球共10个,这些球除颜色外都相同,如果不将球倒出来数,那么你能设计一个试验方案,估计其中红球和白球的比例吗?分析 假设摸了100次,有70次摸到红球,则摸到红球的频率为0.7,根据利用频率估计概率得到摸到红球的概率为0.7,然后根据概率公式可估计这个口袋中红球的数量,再计算白球的数量.
解答 解:假设共摸了100次,有70次摸到红球,所以摸到红球的频率=$\frac{70}{100}$=0.7,由此可根据摸到红球的概率为0.7,所以可估计这个口袋中红球的数量为0.7×10=7(个),则这个口袋中白球的数量=10-7=3(个).
所以估计这个口袋中红球和白球的数量分别为7个、3个.
点评 本题考查了利用频率估计概率:大量重复实验时,事件发生的频率在某个固定位置左右摆动,并且摆动的幅度越来越小,根据这个频率稳定性定理,可以用频率的集中趋势来估计概率,这个固定的近似值就是这个事件的概率.用频率估计概率得到的是近似值,随实验次数的增多,值越来越精确.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
7.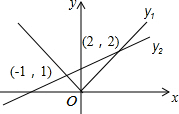 函数y1=|x|,y2=$\frac{1}{3}$x+$\frac{4}{3}$.当y1<y2时,x的范围是( )
函数y1=|x|,y2=$\frac{1}{3}$x+$\frac{4}{3}$.当y1<y2时,x的范围是( )
 函数y1=|x|,y2=$\frac{1}{3}$x+$\frac{4}{3}$.当y1<y2时,x的范围是( )
函数y1=|x|,y2=$\frac{1}{3}$x+$\frac{4}{3}$.当y1<y2时,x的范围是( )| A. | x<-1 | B. | -1<x<2 | C. | x<-1或x>2 | D. | x>2 |
11.某校九年级(8)班50名学生的年龄情况如下表所示:
则从该班随机地抽取一人,抽到学生的年龄恰好是16岁的概率等于$\frac{2}{5}$.
| 年龄 | 15岁 | 16岁 | 17岁 | 18岁 |
| 人 数 | 7 | 20 | 16 | 7 |
8.下列计算正确的是( )
| A. | 2x+3y=5xy | B. | y3÷y3=1 | C. | $\sqrt{2}+\sqrt{3}=\sqrt{5}$ | D. | -$\sqrt{(-4)^{2}}$=-4 |
 如图,正方形网格中每个小正方形的边长都是1,每个小正方形的顶点叫做格点,试画出一个顶点都在格点上,且面积为5的正方形.
如图,正方形网格中每个小正方形的边长都是1,每个小正方形的顶点叫做格点,试画出一个顶点都在格点上,且面积为5的正方形.