题目内容
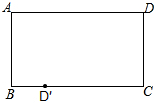 有一张矩形纸片ABCD,要将点D沿某条直线MN翻折180°,恰好落在BC边上的点D′处,MN与AD交于点M,与BC交于点N.
有一张矩形纸片ABCD,要将点D沿某条直线MN翻折180°,恰好落在BC边上的点D′处,MN与AD交于点M,与BC交于点N.(1)请在图中作出该直线MN(保留作图痕迹,不写作法).
(2)分别连接MD′、ND,求证:四边形MD′ND是菱形.
考点:矩形的性质,菱形的判定,翻折变换(折叠问题)
专题:作图题,证明题
分析:(1)连接DD′,作DD′的中垂线分别交AD,BC于点M,N,MN就是所求的直线.
(2)连接MD′、ND,先证出△ODM≌△OD′N,得出四边形MD′ND是平行四边形,再由MN⊥DD′,即可得出四边形MD′ND是菱形.′
(2)连接MD′、ND,先证出△ODM≌△OD′N,得出四边形MD′ND是平行四边形,再由MN⊥DD′,即可得出四边形MD′ND是菱形.′
解答:解:(1)如图所示.

(2)连接MD′、ND,
∵AD∥BC,
∴∠MDD′=∠ND′D,∠DMN=∠MND′,
在△ODM和△OD′N中,
,
∴△ODM≌△OD′N(AAS)
∴DM=DN',
∴四边形MD′ND是平行四边形,
∵MN⊥DD′,
∴四边形MD′ND是菱形.

(2)连接MD′、ND,
∵AD∥BC,
∴∠MDD′=∠ND′D,∠DMN=∠MND′,
在△ODM和△OD′N中,
|
∴△ODM≌△OD′N(AAS)
∴DM=DN',
∴四边形MD′ND是平行四边形,
∵MN⊥DD′,
∴四边形MD′ND是菱形.
点评:本题主要考查了矩形的性质,菱形的判定及翻折变换,解题的关键是正确画出图形,证得△ODM≌△OD′N.

练习册系列答案
相关题目
?ABCD的对角线AC、BD相交于O,AC=4,BD=5,BC=3,则△BOC的周长为( )
| A、7.5 | B、12 |
| C、6 | D、无法确定 |
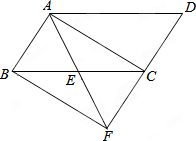 如图,在?ABCD中,E是BC的中点,连结AE并延长,交DC的延长线于点F.
如图,在?ABCD中,E是BC的中点,连结AE并延长,交DC的延长线于点F.