题目内容
如图,在△ABC中,已知AB=BC=CA=4cm,AD⊥BC于D,点P、Q分别从B、C两点同时出发,其中点P沿BC向终点C运动,速度为1cm/s;点Q沿CA、AB向终点B运动,速度为2cm/s,设它们运动的时间为x(s).
(1)求x为何值时,PQ⊥AC;
(2)当0<x<2时,求证:AD平分△PQD的面积;
(3)①设△PQD的面积为y(cm2),求y关于x的函数关系式,及自变量x的取值范围.
②△PQD的面积是否有最大值?若有,请求出这个最大值,及此时x的值;若没有,请说明理由.
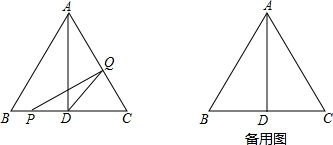
(1)求x为何值时,PQ⊥AC;
(2)当0<x<2时,求证:AD平分△PQD的面积;
(3)①设△PQD的面积为y(cm2),求y关于x的函数关系式,及自变量x的取值范围.
②△PQD的面积是否有最大值?若有,请求出这个最大值,及此时x的值;若没有,请说明理由.
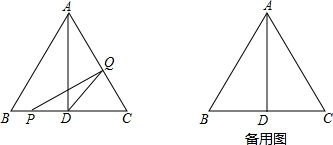
考点:二次函数综合题
专题:
分析:(1)若使PQ⊥AC,则根据路程=速度×时间表示出CP和CQ的长,再根据30度的直角三角形的性质列方程求解;
(2)根据三角形的面积公式,要证明AD平分△PQD的面积,只需证明O是PQ的中点.再根据平行线等分线段定理即可证明;
(3)①根据CQ=2t,∠C=60°,得出QE=CQ•sin60°=
x,进而求出面积即可,②利用二次函数的性质即可求出△PQD面积的最大值.
(2)根据三角形的面积公式,要证明AD平分△PQD的面积,只需证明O是PQ的中点.再根据平行线等分线段定理即可证明;
(3)①根据CQ=2t,∠C=60°,得出QE=CQ•sin60°=
| 3 |
解答:(1)解:当Q在AC上时,由题意得,BP=t,CQ=2t,PC=4-t;
∵AB=BC=CA=4,
∴∠C=60°;
若PQ⊥AC,则有∠QPC=30°,
∴PC=2CQ,
∴4-t=2×2t,
∴t=
;
当Q在AB上时,由题意得,BP=t,AQ=2t-4,则BQ=4-(2t-4)=8-2t,
∵AB=BC=CA=4,∴∠B=60°;
若PQ⊥AB,则有∠QPB=30°,
∴PB=2BQ,
∴t=2(8-2t),
解得:t=
(满足条件2≤t≤4),
即当t=
时,PQ⊥AB;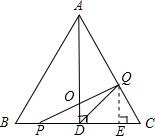
(2)证明:作QE⊥DC于E,
当0<t<2时,点P在BD上,在△QPC中,QC=2t,∠C=60°;
∵QE⊥DC,
∴EC=
QC=t,
∴BP=EC,
∵BD=CD.
∴DP=DE;
∵AD⊥BC,QE⊥BC,
∴∠ADC=∠QEC,
∴AD∥QE,
∴OP=OQ,
∴S△PDO=S△DQO,
∴AD平分△PQD的面积;
(3)①解:∵当0<t<2时,
CQ=2t,∠C=60°,
∴QE=CQ•sin60°=
t,
PD=2-t,
∴△PQD的面积为:y=
×PD×EQ=
(2-t)•
t=-
t2+
t=-
(t-1)2+
,
②△PQD的面积有最大值,
理由如下:由①可知y=
×PD×EQ=
(2-t)•
t=-
t2+
t=-
(t-1)2+
,
∴当t=1时,△PQD面积有最大值为:
.
∵AB=BC=CA=4,
∴∠C=60°;
若PQ⊥AC,则有∠QPC=30°,
∴PC=2CQ,
∴4-t=2×2t,
∴t=
| 4 |
| 5 |
当Q在AB上时,由题意得,BP=t,AQ=2t-4,则BQ=4-(2t-4)=8-2t,
∵AB=BC=CA=4,∴∠B=60°;
若PQ⊥AB,则有∠QPB=30°,
∴PB=2BQ,
∴t=2(8-2t),
解得:t=
| 16 |
| 5 |
即当t=
| 16 |
| 5 |

(2)证明:作QE⊥DC于E,
当0<t<2时,点P在BD上,在△QPC中,QC=2t,∠C=60°;
∵QE⊥DC,
∴EC=
| 1 |
| 2 |
∴BP=EC,
∵BD=CD.
∴DP=DE;
∵AD⊥BC,QE⊥BC,
∴∠ADC=∠QEC,
∴AD∥QE,
∴OP=OQ,
∴S△PDO=S△DQO,
∴AD平分△PQD的面积;
(3)①解:∵当0<t<2时,
CQ=2t,∠C=60°,
∴QE=CQ•sin60°=
| 3 |
PD=2-t,
∴△PQD的面积为:y=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| ||
| 2 |
| 3 |
| ||
| 2 |
| ||
| 2 |
②△PQD的面积有最大值,
理由如下:由①可知y=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| ||
| 2 |
| 3 |
| ||
| 2 |
| ||
| 2 |
∴当t=1时,△PQD面积有最大值为:
| ||
| 2 |
点评:此题主要考查了相似三角形的判定与性质以及三角形的面积求法,综合运用了等边三角形的性质、直角三角形的性质,解题的关键是用动点的时间x和速度表示线段的长度,本题有一定的综合性,难度中等.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
根据下列条件可以列出一元一次方程的是( )
| A、x与1的差的一半 | ||||
| B、一个数的两倍比-2小3 | ||||
C、x的
| ||||
| D、a与b的平方和 |
 如图,三角形纸片ABC,AB=10cm,BC=7cm,AC=6cm,沿过点B的直线折叠这个三角形,使顶点C落在AB边上的点E处,折痕为BD,则△AED的周长为( )
如图,三角形纸片ABC,AB=10cm,BC=7cm,AC=6cm,沿过点B的直线折叠这个三角形,使顶点C落在AB边上的点E处,折痕为BD,则△AED的周长为( )| A、9cm | B、13cm |
| C、16cm | D、10cm |
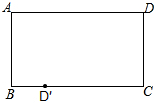 有一张矩形纸片ABCD,要将点D沿某条直线MN翻折180°,恰好落在BC边上的点D′处,MN与AD交于点M,与BC交于点N.
有一张矩形纸片ABCD,要将点D沿某条直线MN翻折180°,恰好落在BC边上的点D′处,MN与AD交于点M,与BC交于点N. 如图是一个几何体的二视图,求该几何体的体积(л取3.14,单位:cm)
如图是一个几何体的二视图,求该几何体的体积(л取3.14,单位:cm)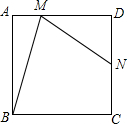 如图,在正方形ABCD中,N是DC的中点,M是AD上异于D点的任一点,且∠NMB=∠MBC.
如图,在正方形ABCD中,N是DC的中点,M是AD上异于D点的任一点,且∠NMB=∠MBC.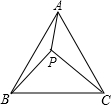 如图,已知点P是等边△ABC内一点,PA=3,PB=4,PC=5,求∠APB的度数.
如图,已知点P是等边△ABC内一点,PA=3,PB=4,PC=5,求∠APB的度数.