题目内容
在一次捐书活动中,七年一班的一个学习小队的学生踊跃参与,甲组同学每人捐献14本书,乙组同学每人捐献15本书,丙组同学每人捐献16本书,三个组的捐书的总数是180个,问该小队共有多少名同学?
考点:一元一次不等式组的应用
专题:
分析:设甲组有学生x人,乙组有学生y人,丙组有学生z人.则依据“三个组的捐书的总数是180个”得到14x+15y+16z=180.根据实际情况知道14x+15y+16z>14x+14y+14z,据此可以求得x+y+z的值.
解答:解:设甲组有学生x人,乙组有学生y人,丙组有学生z人.则
14x+15y+16z=180.
∵14x+15y+16z>14x+14y+14z,14x+15y+16z<16x+16y+16z,
∴
<x+y+z<
,即11
<x+y+z<12
.
∵学生人数是正整数,
∴x+y+z=12.
答:该小队共有人数是12人.
14x+15y+16z=180.
∵14x+15y+16z>14x+14y+14z,14x+15y+16z<16x+16y+16z,
∴
| 180 |
| 14 |
| 180 |
| 16 |
| 1 |
| 4 |
| 6 |
| 7 |
∵学生人数是正整数,
∴x+y+z=12.
答:该小队共有人数是12人.
点评:本题考查了一元一次不等式的应用.此题是把(x+y+z)看作一个整体来解答的.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
下列方程中,两实数根之和等于2的方程是( )
| A、x2+2x-3=0 |
| B、x2-2x+3=0 |
| C、2x2-2x-3=0 |
| D、3x2-6x+1=0 |
根据下列条件可以列出一元一次方程的是( )
| A、x与1的差的一半 | ||||
| B、一个数的两倍比-2小3 | ||||
C、x的
| ||||
| D、a与b的平方和 |
 如图,三角形纸片ABC,AB=10cm,BC=7cm,AC=6cm,沿过点B的直线折叠这个三角形,使顶点C落在AB边上的点E处,折痕为BD,则△AED的周长为( )
如图,三角形纸片ABC,AB=10cm,BC=7cm,AC=6cm,沿过点B的直线折叠这个三角形,使顶点C落在AB边上的点E处,折痕为BD,则△AED的周长为( )| A、9cm | B、13cm |
| C、16cm | D、10cm |
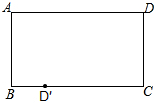 有一张矩形纸片ABCD,要将点D沿某条直线MN翻折180°,恰好落在BC边上的点D′处,MN与AD交于点M,与BC交于点N.
有一张矩形纸片ABCD,要将点D沿某条直线MN翻折180°,恰好落在BC边上的点D′处,MN与AD交于点M,与BC交于点N.