题目内容
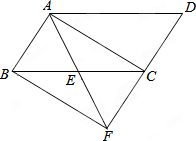 如图,在?ABCD中,E是BC的中点,连结AE并延长,交DC的延长线于点F.
如图,在?ABCD中,E是BC的中点,连结AE并延长,交DC的延长线于点F.(1)求证:△ABE≌△FCE;
(2)当BC与AF满足什么条件时,四边形ABFC是矩形?并说明理由.
考点:平行四边形的性质,全等三角形的判定与性质,矩形的判定
专题:
分析:(1)根据平行四边形的性质得到两角一边对应相等,利用AAS判定△ABE≌△FCE;
(2)由已知可得四边形ABFC是平行四边形,BC=AF,根据对角线相等的平行四边形是矩形,可得到四边形ABFC是矩形.
(2)由已知可得四边形ABFC是平行四边形,BC=AF,根据对角线相等的平行四边形是矩形,可得到四边形ABFC是矩形.
解答:(1)证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∴∠BAE=∠CFE,∠ABE=∠FCE,
∵E为BC的中点,
∴EB=EC.
在△ABE和△FCE中,
,
∴△ABE≌△FCE;
(2)解:当BC=AF时,四边形ABFC是矩形.
理由如下:∵AB∥CF,AB=CF,
∴四边形ABFC是平行四边形,
∵BC=AF,
∴四边形ABFC是矩形.
∴AB∥CD,AB=CD,
∴∠BAE=∠CFE,∠ABE=∠FCE,
∵E为BC的中点,
∴EB=EC.
在△ABE和△FCE中,
|
∴△ABE≌△FCE;
(2)解:当BC=AF时,四边形ABFC是矩形.
理由如下:∵AB∥CF,AB=CF,
∴四边形ABFC是平行四边形,
∵BC=AF,
∴四边形ABFC是矩形.
点评:此题主要考查了学生对全等三角形的判定,平行四边形的性质及矩形的判定等知识点的掌握情况.

练习册系列答案
相关题目
 如图,三角形纸片ABC,AB=10cm,BC=7cm,AC=6cm,沿过点B的直线折叠这个三角形,使顶点C落在AB边上的点E处,折痕为BD,则△AED的周长为( )
如图,三角形纸片ABC,AB=10cm,BC=7cm,AC=6cm,沿过点B的直线折叠这个三角形,使顶点C落在AB边上的点E处,折痕为BD,则△AED的周长为( )| A、9cm | B、13cm |
| C、16cm | D、10cm |
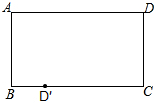 有一张矩形纸片ABCD,要将点D沿某条直线MN翻折180°,恰好落在BC边上的点D′处,MN与AD交于点M,与BC交于点N.
有一张矩形纸片ABCD,要将点D沿某条直线MN翻折180°,恰好落在BC边上的点D′处,MN与AD交于点M,与BC交于点N.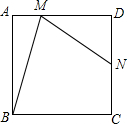 如图,在正方形ABCD中,N是DC的中点,M是AD上异于D点的任一点,且∠NMB=∠MBC.
如图,在正方形ABCD中,N是DC的中点,M是AD上异于D点的任一点,且∠NMB=∠MBC.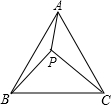 如图,已知点P是等边△ABC内一点,PA=3,PB=4,PC=5,求∠APB的度数.
如图,已知点P是等边△ABC内一点,PA=3,PB=4,PC=5,求∠APB的度数. 如图,已知直线AB、CD相交于点O,OB平分∠DOE,∠DOE=80°,则∠AOC=
如图,已知直线AB、CD相交于点O,OB平分∠DOE,∠DOE=80°,则∠AOC= 实数a,b在数轴上的位置如图所示,则
实数a,b在数轴上的位置如图所示,则