题目内容
已知抛物线y=ax2+bx+c与x轴交于A(-1,0)、B(3,0)两点,与y轴交于C点,∠ACB≥90°.
(1)求点C的坐标(用含a的代数式表示);
(2)求a的取值范围;
(3)设D为拋物线的顶点,求△ACD中边CD上的高h的最大值.
(1)求点C的坐标(用含a的代数式表示);
(2)求a的取值范围;
(3)设D为拋物线的顶点,求△ACD中边CD上的高h的最大值.
考点:二次函数综合题
专题:
分析:(1)将A、B的坐标代入抛物线的解析式中,即可求出c的值,也就得出了C点的坐标;
(2)由于抛物线的解析式中二次项系数的绝对值越大开口越小,因此可计算出当∠ACB=90°时a的取值进而来求a的取值范围.当∠ACB=90°时,根据射影定理可求出OC的长,根据(1)中表示C点坐标的式子可得出此时a的值.因此a的取值范围就应该是0到这个值之间(a≠0);
(3)延长DC交x轴于H,过A作AM⊥DH于M,那么AM就是所求的h;先根据抛物线的解析式求出抛物线的顶点坐标,过D作DG⊥y轴于G,根据相似三角形DCG和HCO不难求出OH=3,那么AH=2,因此在直角三角形HAM中,要想使AM最长,就需要使∠OHC最大,即OC要最长,根据(2)a的取值范围即可得出a的最大值,也就能求出此时∠AHM的正弦值,进而可求出AM的最大值.
(2)由于抛物线的解析式中二次项系数的绝对值越大开口越小,因此可计算出当∠ACB=90°时a的取值进而来求a的取值范围.当∠ACB=90°时,根据射影定理可求出OC的长,根据(1)中表示C点坐标的式子可得出此时a的值.因此a的取值范围就应该是0到这个值之间(a≠0);
(3)延长DC交x轴于H,过A作AM⊥DH于M,那么AM就是所求的h;先根据抛物线的解析式求出抛物线的顶点坐标,过D作DG⊥y轴于G,根据相似三角形DCG和HCO不难求出OH=3,那么AH=2,因此在直角三角形HAM中,要想使AM最长,就需要使∠OHC最大,即OC要最长,根据(2)a的取值范围即可得出a的最大值,也就能求出此时∠AHM的正弦值,进而可求出AM的最大值.
解答:解:(1)∵抛物线y=ax2+bx+c过点A(-1,0),B(3,0),
∴
,
消去b,得c=-3a
∴C的坐标为(0,-3a);
(2)当∠ACB=90°时,∠AOC=∠BOC=90°,
∴∠OBC+∠BCO=90°,∠ACO+∠BCO=90°,
∴∠ACO=∠OBC,
∴△AOC∽△COB
∴
=
,
∴OC2=AO•OB,
∵AO=1,OB=3,
∴OC=
,
∵∠ACB≥90°,
∴OC≤
,
若a>0,则-c≤
,
由(1)得3a≤
,
∴a≤
,
∴a的取值范围为:0<a≤
;
若a<0,则c≤
,
即-3a≤
,
∴a≥-
,
∴a的取值范围为:-
≤a<0;
综上可得:a的取值范围为:0<a≤
或-
≤a<0;
(3)作DG⊥y轴于点G,延长DC交x轴于点H,如图,
∵抛物线y=ax2+bx+c交x轴于A(-1,0),B(3,0),
∴抛物线的对称轴为x=1,
即-
=1,
∴b=-2a,
又由(1)有c=-3a,
∴抛物线方程为:y=ax2-2ax-3a,
∴D点坐标为(1,-4a),
∴CO=|3a|,GC=|a|,DG=1,
∵DG∥OH,
∴△DCG∽△HCO,
∴
=
,即
=
,
∴OH=3,
∴直线DC过定点H(-3,0),
∴AH=2,
过A作AM⊥DH,垂足为M,即AM=h,
∴h=HAsin∠OHC=2sin∠OHC,
∵0<CO≤
,
∴0°<∠OHC≤30°,
∴0<sin∠OHC≤
,
∴0<h≤1,
∴h的最大值为1.
∴
|
消去b,得c=-3a
∴C的坐标为(0,-3a);
(2)当∠ACB=90°时,∠AOC=∠BOC=90°,
∴∠OBC+∠BCO=90°,∠ACO+∠BCO=90°,
∴∠ACO=∠OBC,
∴△AOC∽△COB
∴
| AO |
| OC |
| OC |
| OB |
∴OC2=AO•OB,
∵AO=1,OB=3,
∴OC=
| 3 |
∵∠ACB≥90°,
∴OC≤
| 3 |
若a>0,则-c≤
| 3 |
由(1)得3a≤
| 3 |
∴a≤
| ||
| 3 |
∴a的取值范围为:0<a≤
| ||
| 3 |
若a<0,则c≤
| 3 |
即-3a≤
| 3 |
∴a≥-
| ||
| 3 |
∴a的取值范围为:-
| ||
| 3 |
综上可得:a的取值范围为:0<a≤
| ||
| 3 |
| ||
| 3 |
(3)作DG⊥y轴于点G,延长DC交x轴于点H,如图,
∵抛物线y=ax2+bx+c交x轴于A(-1,0),B(3,0),
∴抛物线的对称轴为x=1,
即-
| b |
| 2a |
∴b=-2a,
又由(1)有c=-3a,
∴抛物线方程为:y=ax2-2ax-3a,
∴D点坐标为(1,-4a),
∴CO=|3a|,GC=|a|,DG=1,
∵DG∥OH,

∴△DCG∽△HCO,
∴
| DG |
| OH |
| GC |
| CO |
| 1 |
| OH |
| |a| |
| |3a| |
∴OH=3,
∴直线DC过定点H(-3,0),
∴AH=2,
过A作AM⊥DH,垂足为M,即AM=h,
∴h=HAsin∠OHC=2sin∠OHC,
∵0<CO≤
| 3 |
∴0°<∠OHC≤30°,
∴0<sin∠OHC≤
| 1 |
| 2 |
∴0<h≤1,
∴h的最大值为1.
点评:此题属于二次函数的综合题,考查了待定系数求函数解析式、相似三角形的判定与性质以及锐角三角函数的知识.此题难度较大,综合性较强,注意掌握数形结合思想与方程思想的应用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
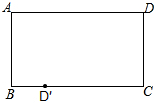 有一张矩形纸片ABCD,要将点D沿某条直线MN翻折180°,恰好落在BC边上的点D′处,MN与AD交于点M,与BC交于点N.
有一张矩形纸片ABCD,要将点D沿某条直线MN翻折180°,恰好落在BC边上的点D′处,MN与AD交于点M,与BC交于点N. 如图是一个几何体的二视图,求该几何体的体积(л取3.14,单位:cm)
如图是一个几何体的二视图,求该几何体的体积(л取3.14,单位:cm)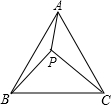 如图,已知点P是等边△ABC内一点,PA=3,PB=4,PC=5,求∠APB的度数.
如图,已知点P是等边△ABC内一点,PA=3,PB=4,PC=5,求∠APB的度数.