题目内容
阅读下列文字与例题:
将一个多项式分组后,可提公因式或运用公式继续分解的方法是分组分解法.
例如:
(1)am+an+bm+bn=(am+bm)+(an+bn)=m(a+b)+n(a+b)=(a+b)(m+n);
(2)x2-y2-2y-1=x2-(y2+2y+1)=x2-(y+1)2=(x+y+1)(x-y-1).
试用上述方法分解因式:
(1)a2+2ab+ac+bc+b2;
(2)4-x2+4xy-4y2.
将一个多项式分组后,可提公因式或运用公式继续分解的方法是分组分解法.
例如:
(1)am+an+bm+bn=(am+bm)+(an+bn)=m(a+b)+n(a+b)=(a+b)(m+n);
(2)x2-y2-2y-1=x2-(y2+2y+1)=x2-(y+1)2=(x+y+1)(x-y-1).
试用上述方法分解因式:
(1)a2+2ab+ac+bc+b2;
(2)4-x2+4xy-4y2.
考点:因式分解-分组分解法
专题:阅读型
分析:(1)a2+2ab+ac+bc+b2可以进行分组变成(a2+2ab+b2)+(ac+bc),则前边括号内的三项可以利用完全平方公式分解,后边的三项可以提公因式,然后再利用提公因式法即可分解;
(2)将后三项为一组运用完全平方公式,再运用平方差公式分解因式即可.
(2)将后三项为一组运用完全平方公式,再运用平方差公式分解因式即可.
解答:解:(1)a2+2ab+ac+bc+b2
=a2+2ab+b2+ac+bc
=(a+b)2+c(a+b)
=(a+b)(a+b+c);
(2)4-x2+4xy-4y2
=4-(x2-4xy+4y2)
=4-(x-2y)2
=(2-x+2y)(2-x+2y).
=a2+2ab+b2+ac+bc
=(a+b)2+c(a+b)
=(a+b)(a+b+c);
(2)4-x2+4xy-4y2
=4-(x2-4xy+4y2)
=4-(x-2y)2
=(2-x+2y)(2-x+2y).
点评:本题考查了分组分解法分解因式,难点是采用两两分组还是三一分组.正确分组进而提取公因式是解题关键.

练习册系列答案
相关题目
已知圆的半径为10cm,如果一条直线上的个一点P和圆心O的距离为12cm,那么这条直线和这个圆的位置关系是( )
| A、相离 | B、相交和相切 |
| C、相交 | D、都可能 |
已知抛物线y=x2+x-2与直线y=5x-m没有公共点,则m的取值范围是( )
| A、m<6 | B、m>6 |
| C、m≤6 | D、m≥2 |
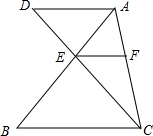 如图所示,在△ABC和△CAD中,DA∥BC,CD交AB于E,且AE:EB=1:2,EF∥BC交AC于F,S△ADE=1,求S△AEF和S△BCE.
如图所示,在△ABC和△CAD中,DA∥BC,CD交AB于E,且AE:EB=1:2,EF∥BC交AC于F,S△ADE=1,求S△AEF和S△BCE.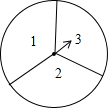 如图,转盘被平均分成三块扇形,转动转盘,转动过程中,指针保持不动,转盘停止后,如果指针恰好指在分割线上,则重转一次,直到指针指向一个数字所在的区域为止.
如图,转盘被平均分成三块扇形,转动转盘,转动过程中,指针保持不动,转盘停止后,如果指针恰好指在分割线上,则重转一次,直到指针指向一个数字所在的区域为止.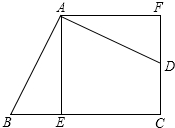 如图,四边形ABCD的∠BAD=∠C=90°,AB=AD,AE⊥BC于E,△BEA旋转后能与△DFA重合.
如图,四边形ABCD的∠BAD=∠C=90°,AB=AD,AE⊥BC于E,△BEA旋转后能与△DFA重合.