题目内容
6.形如x+$\frac{1}{x}$=a$+\frac{1}{a}$的方程的解为:x1=a,x2=$\frac{1}{a}$.解方程:$\frac{{x}^{2}+x+1}{{x}^{2}+1}$$+\frac{2{x}^{2}+x+2}{{x}^{2}+x+1}$=$\frac{19}{6}$.分析 把原方程变形为$\frac{{x}^{2}+x+1}{{x}^{2}+1}$+$\frac{{x}^{2}+1}{{x}^{2}+x+1}$=$\frac{2}{3}$+$\frac{3}{2}$,设y=$\frac{{x}^{2}+x+1}{{x}^{2}+1}$于是得到原方程变为y+$\frac{1}{y}$=$\frac{2}{3}$+$\frac{3}{2}$,求得y1=$\frac{2}{3}$,y2=$\frac{3}{2}$,当$\frac{{x}^{2}+x+1}{{x}^{2}+1}$=$\frac{2}{3}$时,当$\frac{{x}^{2}+x+1}{{x}^{2}+1}$=$\frac{3}{2}$时,即可求得结果.
解答 解:原方程变形为:$\frac{{x}^{2}+x+1}{{x}^{2}+1}$+$\frac{{x}^{2}+1}{{x}^{2}+x+1}$=$\frac{2}{3}$+$\frac{3}{2}$,
设y=$\frac{{x}^{2}+x+1}{{x}^{2}+1}$,则原方程变为y+$\frac{1}{y}$=$\frac{2}{3}$+$\frac{3}{2}$,解得:y1=$\frac{2}{3}$,y2=$\frac{3}{2}$,
当$\frac{{x}^{2}+x+1}{{x}^{2}+1}$=$\frac{2}{3}$时,x=$\frac{-3±\sqrt{5}}{2}$,
当$\frac{{x}^{2}+x+1}{{x}^{2}+1}$=$\frac{3}{2}$时,x=1,
经检验x=$\frac{-3±\sqrt{5}}{2}$和x=1都是原方程的根,
故原方程的根是x=$\frac{-3±\sqrt{5}}{2}$和x=1.
点评 此题考查了解分式方程,利用了转化的思想,解分式方程注意要检验.

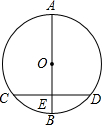 如图,AB是⊙O的直径,弦CD⊥AB于E,CD=16,EB=4,则AE=( )
如图,AB是⊙O的直径,弦CD⊥AB于E,CD=16,EB=4,则AE=( )| A. | 20 | B. | 18 | C. | 16 | D. | 14 |
| A. | a3+a3=2a6 | B. | a2•a3=a6 | C. | (a2)3=a5 | D. | a2÷a5=a-3 |
 如图点C、D在线段AB上,D是线段AB的中点,AC=$\frac{1}{3}$AD,CD=6,求线段AB的长.
如图点C、D在线段AB上,D是线段AB的中点,AC=$\frac{1}{3}$AD,CD=6,求线段AB的长.