题目内容
20．
如图，已知⊙O是△ABD的外接圆，AB是⊙O的直径，CD是⊙O的弦，∠ABD=56°，则∠BCD等于34°．
分析 先根据圆周角定理由AB是⊙O的直径得到∠ADB=90°，再根据互余得到∠A=90°-∠ABD=34°，然后根据圆周角定理求解．
解答 解：∵AB是⊙O的直径，
∴∠ADB=90°，
∴∠A=90°-∠ABD=90°-56°=34°，
∴∠BCD=∠A=34°，
故答案为：34°．
点评 本题考查了圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．推论：半圆（或直径）所对的圆周角是直角，90°的圆周角所对的弦是直径，熟练运用圆周角定理是解答此题的关键．
练习册系列答案
名校课堂系列答案
相关题目
8．正六边形的边心距为$\sqrt{3}$，则该正六边形的外接圆半径为（ ）
| A． | $\sqrt{3}$ | B． | 2 | C． | 3 | D． | 2$\sqrt{3}$ |
15．在下面四个图形中，既是轴对称图形又是中心对称图形的有（ ）
| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
12．
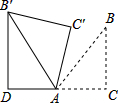如图，△ABC为等腰直角三角形，∠ACB=90°，将△ABC绕点A逆时针旋转75°得到△AB′C′，过点B′作B′D⊥CA，交CA的延长线于点D，若AC=3$\sqrt{2}$，则AD的长为（ ）
如图，△ABC为等腰直角三角形，∠ACB=90°，将△ABC绕点A逆时针旋转75°得到△AB′C′，过点B′作B′D⊥CA，交CA的延长线于点D，若AC=3$\sqrt{2}$，则AD的长为（ ）| A． | 2 | B． | 3 | C． | 2$\sqrt{3}$ | D． | 3$\sqrt{2}$ |
9．“微信发红包”是刚刚兴起的一种娱乐方式，为了解所在单位员工春节期间使用微信发红包的情况，小红随机调查了15名同事，结果如表：
则此次调查中平均每个红包的钱数的众数为2元，中位数为5元．
| 平均每个红包的钱数（元） | 2 | 5 | 10 | 20 | 50 |
| 人数 | 7 | 4 | 2 | 1 | 1 |
