题目内容
8．正六边形的边心距为$\sqrt{3}$，则该正六边形的外接圆半径为（ ）| A． | $\sqrt{3}$ | B． | 2 | C． | 3 | D． | 2$\sqrt{3}$ |
分析 设正六边形的中心是O，一边是AB，过O作OG⊥AB与G，在直角△OAG中，根据三角函数即可求得边长AB，从而求出周长．
解答 
解：如图，
在Rt△AOG中，OG=$\sqrt{3}$，∠AOG=30°，
∴OA=OG÷cos 30°=$\sqrt{3}$÷$\frac{\sqrt{3}}{2}$=2；
故选：B．
点评 本题主要考查正多边形的计算问题，常用的思路是转化为直角三角形中边和角的计算，属于常规题．
练习册系列答案
名校课堂系列答案
相关题目
10．某班七个兴趣小组人数分别为4，4，5，5，x，6，7，已知这组数据的平均数是5，则这组数据的众数和中位数分别是（ ）
| A． | 4，5 | B． | 4，4 | C． | 5，4 | D． | 5，5 |
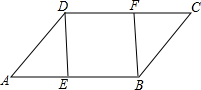如图，已知点E、F分别在?ABCD的边AB、CD上，且AE=CF．求证：DE=BF．
3．
如图是太原市某日八个整点的空气质量趋势图（空气指数越大越严重），根据图中的空气指数可知这组数据的中位数是（ ）
如图是太原市某日八个整点的空气质量趋势图（空气指数越大越严重），根据图中的空气指数可知这组数据的中位数是（ ）| A． | 64 | B． | 60 | C． | 56 | D． | 48 |
如图，已知⊙O是△ABD的外接圆，AB是⊙O的直径，CD是⊙O的弦，∠ABD=56°，则∠BCD等于34°．
如图，平行四边形ABCD中，过A作AM⊥BC于M，交BD于E，过C作CN⊥AD于N，交BD于F，连结AF、CE．