题目内容
12.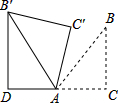 如图,△ABC为等腰直角三角形,∠ACB=90°,将△ABC绕点A逆时针旋转75°得到△AB′C′,过点B′作B′D⊥CA,交CA的延长线于点D,若AC=3$\sqrt{2}$,则AD的长为( )
如图,△ABC为等腰直角三角形,∠ACB=90°,将△ABC绕点A逆时针旋转75°得到△AB′C′,过点B′作B′D⊥CA,交CA的延长线于点D,若AC=3$\sqrt{2}$,则AD的长为( )| A. | 2 | B. | 3 | C. | 2$\sqrt{3}$ | D. | 3$\sqrt{2}$ |
分析 直接利用等腰直角三角形的性质得出∠CAB=∠B=45°,再利用勾股定理得出AB的长,再利用旋转的性质得出AB′的长,再结合直角三角形的性质求出答案.
解答  解:∵△ABC为等腰直角三角形,∠ACB=90°,
解:∵△ABC为等腰直角三角形,∠ACB=90°,
∴∠CAB=∠B=45°,
∵AC=BC=3$\sqrt{2}$,
∴AB=6,
∵将△ABC绕点A逆时针旋转75°得到△AB′C′,
∴∠B′AB=75°,AB′=6,
∴∠DAB′=180°-75°-45°=60°,
∵B′D⊥CA,
∴∠DB′A=30°,
∴AD=$\frac{1}{2}$AB′=3.
故选:B.
点评 此题主要考查了旋转的性质以及勾股定理、等腰直角三角形的性质等知识,正确得出AB′的长是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3. 如图是太原市某日八个整点的空气质量趋势图(空气指数越大越严重),根据图中的空气指数可知这组数据的中位数是( )
如图是太原市某日八个整点的空气质量趋势图(空气指数越大越严重),根据图中的空气指数可知这组数据的中位数是( )
 如图是太原市某日八个整点的空气质量趋势图(空气指数越大越严重),根据图中的空气指数可知这组数据的中位数是( )
如图是太原市某日八个整点的空气质量趋势图(空气指数越大越严重),根据图中的空气指数可知这组数据的中位数是( )| A. | 64 | B. | 60 | C. | 56 | D. | 48 |
7.十边形的内角和为( )
| A. | 360° | B. | 1440° | C. | 1800° | D. | 2160° |
1.下列调查中,最合适采用抽样调查的是( )
| A. | 乘坐高铁对旅客的行李的检查 | |
| B. | 了解抚顺市民对春节晚会节目的满意程度 | |
| C. | 调查九年一班全体同学的身高情况 | |
| D. | 对新研发的新型战斗机的零部件进行检查 |
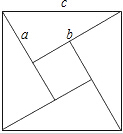 2002年8月在北京召开的国际数学家大会会徽取材于我国古代数学家赵爽的弦图,它是由四个全等的直角三角形和中间的小正方形拼成的一个大正方形,如图所示,如果小正方形的面积为3,直角三角形中较小的锐角为30°,那么大正方形的面积为12+6$\sqrt{3}$.
2002年8月在北京召开的国际数学家大会会徽取材于我国古代数学家赵爽的弦图,它是由四个全等的直角三角形和中间的小正方形拼成的一个大正方形,如图所示,如果小正方形的面积为3,直角三角形中较小的锐角为30°,那么大正方形的面积为12+6$\sqrt{3}$. 如图,已知⊙O是△ABD的外接圆,AB是⊙O的直径,CD是⊙O的弦,∠ABD=56°,则∠BCD等于34°.
如图,已知⊙O是△ABD的外接圆,AB是⊙O的直径,CD是⊙O的弦,∠ABD=56°,则∠BCD等于34°. 如图,平行四边形ABCD中,过A作AM⊥BC于M,交BD于E,过C作CN⊥AD于N,交BD于F,连结AF、CE.
如图,平行四边形ABCD中,过A作AM⊥BC于M,交BD于E,过C作CN⊥AD于N,交BD于F,连结AF、CE.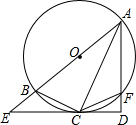 如图,已知AB为⊙O的直径,F为⊙O上一点,AC平分∠BAF且交⊙O于点C,过点C作CD⊥AF于点D,延长AB、DC交于点E,连接BC、CF.
如图,已知AB为⊙O的直径,F为⊙O上一点,AC平分∠BAF且交⊙O于点C,过点C作CD⊥AF于点D,延长AB、DC交于点E,连接BC、CF.