题目内容
20. 如图,已知:点E是正方形ABCD的BC边上的点,现将△DCE沿折痕DE向上翻折,使DC落在对角线DB上,则CD:CE==($\sqrt{2}$+1):1.
如图,已知:点E是正方形ABCD的BC边上的点,现将△DCE沿折痕DE向上翻折,使DC落在对角线DB上,则CD:CE==($\sqrt{2}$+1):1.
分析 设CE=1,由翻折性质知,EF=EC=1,由正方形性质得到∠EBF=45°,得到BF=EF=1,由勾股定理得到BE=$\sqrt{2}$,从而推得BC=$\sqrt{2}$+1,于是得到结论.
解答 解:设点C落在BD上的点F处,
则∠BFE=∠C=90°
设CE=1,
则EF=EC=1
∵ABCD是正方形
∴∠EBF=45°
∴BF=EF=1
∴BE=$\sqrt{2}$,
∴CD=BC=$\sqrt{2}$+1,
∴CD:CE=($\sqrt{2}$+1):1,
故答案为:=($\sqrt{2}$+1):1.
点评 本题主要考查了翻折的性质,正方形的性质,勾股定理等知识,熟练掌握翻折的性质,利用勾股定理求得BE=$\sqrt{2}$是解决问题的关键.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
15.下列各数中,最小的实数是( )
| A. | 0 | B. | π | C. | -$\sqrt{2}$ | D. | -1 |
5.函数y=$\frac{\sqrt{x-3}}{x-3}$中自变量x的取值范围正确的是( )
| A. | x>3 | B. | x≥3 | C. | x<3 | D. | x≤3 |
10.已知一次函数y=-2x+3,则与该一次函数的图象关于x轴对称的一次函数的表达式为( )
| A. | y=2x-3 | B. | y=-2x-3 | C. | y=2x+3 | D. | y=-2x+3 |
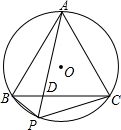 如图,P为正三角形ABC的外接圆O的劣弧BC上的任意一点,PA与BC交于D,连接PB、PC
如图,P为正三角形ABC的外接圆O的劣弧BC上的任意一点,PA与BC交于D,连接PB、PC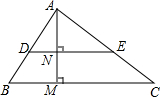 如图,已知△ADE∽△ABC,且AD=3,BD=2.若AM⊥BC于M,AM交DE于N,AM=4,则AN=$\frac{12}{5}$.
如图,已知△ADE∽△ABC,且AD=3,BD=2.若AM⊥BC于M,AM交DE于N,AM=4,则AN=$\frac{12}{5}$.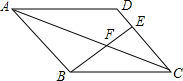 如图,在平行四边形ABCD中,E在DC上,若BF:BE=4:7,则DE:EC=1:3.
如图,在平行四边形ABCD中,E在DC上,若BF:BE=4:7,则DE:EC=1:3.