题目内容
5.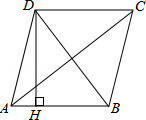 如图,四边形ABCD是菱形,AC=8,DB=6,DH⊥AB于H,则DH=( )
如图,四边形ABCD是菱形,AC=8,DB=6,DH⊥AB于H,则DH=( )| A. | $\frac{24}{5}$ | B. | $\frac{12}{5}$ | C. | 4 | D. | 8 |
分析 由四边形ABCD是菱形,AC=8,DB=6,可求得此菱形的面积与AB的长,继而求得答案.
解答  解:设AC与BD交于O,
解:设AC与BD交于O,
∵四边形ABCD是菱形,AC=8,DB=6,
∴AC⊥BD,OA=$\frac{1}{2}$AC=4,OB=$\frac{1}{2}$BD=3,
∴AB=$\sqrt{O{A}^{2}+O{B}^{2}}$=5,S菱形ABCD=$\frac{1}{2}$AC•BD=24,
∵DH⊥AB,
∴DH=$\frac{{S}_{菱形ABCD}}{AB}$=$\frac{24}{5}$.
故选A.
点评 此题考查了菱形的性质以及勾股定理.注意菱形的面积等于对角线积的一半或底乘以高.

练习册系列答案
 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
8.下列各式计算正确的是( )
| A. | (a+2)(a-2)=4-a2 | B. | (a+2b)2=a2+2ab+4b2 | ||
| C. | (-x-y)2=x2-2xy-y2 | D. | (4ab+1)(4ab-1)=16a2b2-1 |
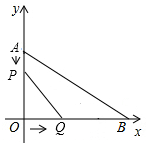 如图,在平面直角坐标系中,已知点A(0,6),B(8,0).点P从A点出发,以每秒1个单位的速度沿AO运动;同时,点Q从O出发,以每秒2个单位的速度沿OB运动,当Q点到达B点时,P、Q两点同时停止运动.
如图,在平面直角坐标系中,已知点A(0,6),B(8,0).点P从A点出发,以每秒1个单位的速度沿AO运动;同时,点Q从O出发,以每秒2个单位的速度沿OB运动,当Q点到达B点时,P、Q两点同时停止运动.