题目内容
8．下列各式计算正确的是（ ）| A． | （a+2）（a-2）=4-a2 | B． | （a+2b）2=a2+2ab+4b2 | ||
| C． | （-x-y）2=x2-2xy-y2 | D． | （4ab+1）（4ab-1）=16a2b2-1 |
分析 原式各项利用平方差公式及完全平方公式化简得到结果，即可作出判断．
解答 解：A、原式=a2-4，错误；
B、原式=a2+4ab+4b2，错误；
C、原式=x2+2xy+y2，错误；
D、原式=16a2b2-1，正确，
故选D
点评 此题考查了平方差公式，以及完全平方公式，熟练掌握公式是解本题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
18．如果不等式组$\left\{\begin{array}{l}x＞-2\\ x≤m\end{array}\right.$的整数解共有3个，则m的取值范围是（ ）
| A． | 1＜m＜2 | B． | 1≤m＜2 | C． | 1＜m≤2 | D． | 1≤m≤2 |
19．下列式子中，属于最简二次根式的是（ ）
| A． | $\sqrt{\frac{1}{2}}$ | B． | $\frac{{\sqrt{5}}}{2}$ | C． | $\sqrt{0.5}$ | D． | $\sqrt{12}$ |
3．使分式$\frac{2}{x+1}$有意义的x的取值范围为（ ）
| A． | x≠1 | B． | x≠-1 | C． | x≠0 | D． | x≠±1 |
5．
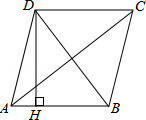如图，四边形ABCD是菱形，AC=8，DB=6，DH⊥AB于H，则DH=（ ）
如图，四边形ABCD是菱形，AC=8，DB=6，DH⊥AB于H，则DH=（ ）| A． | $\frac{24}{5}$ | B． | $\frac{12}{5}$ | C． | 4 | D． | 8 |
3．下列计算中，错误的是（ ）
| A． | 5a3-a3=4a3 | B． | 2n•3n=6n+n | C． | （a-b）3•（b-a）2=（a-b）5 | D． | -a2•（-a）3=a5 |