题目内容
10.解方程(组)(1)3y-2=5y+2; (2)$\frac{x+2}{4}-\frac{x-1}{2}$=1;(3)$\left\{\begin{array}{l}{3(x+y)-4(x-y)=4}\\{\frac{x+y}{2}+\frac{x-y}{6}=1}\end{array}$.
分析 (1)直接按移项、合并同类项、系数化为1解方程即可;
(2)先去分母,再化简解方程,注意不能漏乘4;
(3)先去括号、去分母化成整式方程,再利用代入消元法解方程组,也可以用加减法解.
解答 解:(1)3y-2=5y+2,
移项,得:3y-5y=2+2,
合并同类项,得:-2y=4,
未知数系数化成1,得:y=-2;
(2)$\frac{x+2}{4}-\frac{x-1}{2}$=1,
解:去分母,得:(x+2)-2(x-1)=4,
去括号,得:x+2-2x+2=4,
移项、合并,得:-x=0,
x=0;
(3)$\left\{\begin{array}{l}{3(x+y)-4(x-y)=4}\\{\frac{x+y}{2}+\frac{x-y}{6}=1}\end{array}$,
解:整理,得:$\left\{\begin{array}{l}{-x+7y=4①}\\{2x+y=3②}\end{array}\right.$,
由①得:x=7y-4③,
把③代入②得:2(7y-4)+y=3,$y=\frac{11}{15}$,
把y=$\frac{11}{15}$代入③得:x=$\frac{17}{15}$,
∴$\left\{\begin{array}{l}{x=\frac{17}{15}}\\{y=\frac{11}{15}}\end{array}\right.$.
点评 本题考查了一元一次方程和二元一次方程组,属于基础题,做好此题要明确以下知识:
①解一元一次方程的一般步骤:去分母、去括号、移项、合并同类项、系数化为1;
②解二元一次方程组的方法:用代入法或加减法解二元一次方程组.

练习册系列答案
 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
15.一组数据:2、2、3、3、3、4、4中位数是( )
| A. | 2 | B. | 3 | C. | 3.5 | D. | 4 |
5.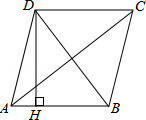 如图,四边形ABCD是菱形,AC=8,DB=6,DH⊥AB于H,则DH=( )
如图,四边形ABCD是菱形,AC=8,DB=6,DH⊥AB于H,则DH=( )
 如图,四边形ABCD是菱形,AC=8,DB=6,DH⊥AB于H,则DH=( )
如图,四边形ABCD是菱形,AC=8,DB=6,DH⊥AB于H,则DH=( )| A. | $\frac{24}{5}$ | B. | $\frac{12}{5}$ | C. | 4 | D. | 8 |
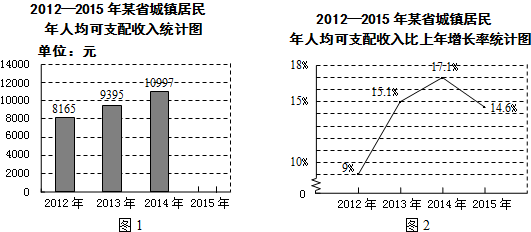
 某市有A,B,C,D,E五个景点,该市旅游局对某月进入景点的人数的情况进行调查统计,并将统计结果绘制成如图所示的两幅不完整的统计图.
某市有A,B,C,D,E五个景点,该市旅游局对某月进入景点的人数的情况进行调查统计,并将统计结果绘制成如图所示的两幅不完整的统计图.