题目内容
2. 如图,反比例函数y=$\frac{6}{x}$在一象限的图象上有两点A,B,它们的横坐标分别为1,3,则△OAB的面积为8.
如图,反比例函数y=$\frac{6}{x}$在一象限的图象上有两点A,B,它们的横坐标分别为1,3,则△OAB的面积为8.
分析 根据题意结合反比例函数图象上点的坐标性质S△ACO=S△OBD=3,得出S四边形AODB的值是解题关键.
解答 解:如图所示: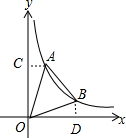
过点A作AC⊥y轴于点C,过点B作BD⊥x轴于点D,
∵反比例函数y=$\frac{6}{x}$在第一象限的图象上有两点A,B,它们的横坐标分别是2,6,
∴x=1时,y=6;x=3时,y=2,
故S△ACO=S△OBD=3,
S四边形AODB=$\frac{1}{2}$×(3+1)×4+3=11,
故△AOB的面积是:11-3=8.
故答案为:8.
点评 此题主要考查了反比例函数图象上点的坐标性质,得出四边形AODB的面积是解题关键.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
17. 如图,在△ABC中,点D是BC的中点,点E、F分别在线段AD及其延长线上,且DE=DF.下列条件使四边形BECF为菱形的是( )
如图,在△ABC中,点D是BC的中点,点E、F分别在线段AD及其延长线上,且DE=DF.下列条件使四边形BECF为菱形的是( )
 如图,在△ABC中,点D是BC的中点,点E、F分别在线段AD及其延长线上,且DE=DF.下列条件使四边形BECF为菱形的是( )
如图,在△ABC中,点D是BC的中点,点E、F分别在线段AD及其延长线上,且DE=DF.下列条件使四边形BECF为菱形的是( )| A. | BE⊥CE | B. | BF∥CE | C. | BE=CF | D. | AB=AC |
11.若点(x1,y1),(x2,y2)都是反比例函数y=-$\frac{1}{x}$图象上的点,并且y1<0<y2,则下列结论中正确的是( )
| A. | x1<x2 | B. | x2<x1 | ||
| C. | y随x的增大而增大 | D. | 两点有可能在同一象限 |
12.一枚质地均匀的六面骰子,六个面上分别刻有1,2,3,4,5,6点,投掷一次得到的点数为奇数的概率是( )
| A. | $\frac{1}{6}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
 已知点D是△ABC内一定点,且有∠DAC=∠DCB=∠DBA=30°,求证:△ABC是等边三角形.
已知点D是△ABC内一定点,且有∠DAC=∠DCB=∠DBA=30°,求证:△ABC是等边三角形. 已知:O是坐标原点,P(m,n)(m>0)是函数y=$\frac{k}{x}$(k>0)上的点,过点P作直线PA⊥OP于P,直线PA与x轴的正半轴交于点A(a,0)(a>m).设△OPA的面积为s,且s=1+$\frac{{n}^{4}}{4}$.
已知:O是坐标原点,P(m,n)(m>0)是函数y=$\frac{k}{x}$(k>0)上的点,过点P作直线PA⊥OP于P,直线PA与x轴的正半轴交于点A(a,0)(a>m).设△OPA的面积为s,且s=1+$\frac{{n}^{4}}{4}$. 在平面直角坐标系xOy中,抛物线y=x2+bx+c经过点(0,-3),(2,-3).
在平面直角坐标系xOy中,抛物线y=x2+bx+c经过点(0,-3),(2,-3).