题目内容
7.一组按规律排列的式子:a2,$\frac{{a}^{4}}{3}$,$\frac{{a}^{6}}{5}$,$\frac{{a}^{8}}{7}$,…,则第2016个式子是( )| A. | $\frac{{a}^{2016}}{2015}$ | B. | $\frac{{a}^{2016}}{4029}$ | C. | $\frac{{a}^{4032}}{4031}$ | D. | $\frac{{a}^{4032}}{4029}$ |
分析 根据一组按规律排列的式子:a2,$\frac{{a}^{4}}{3}$,$\frac{{a}^{6}}{5}$,$\frac{{a}^{8}}{7}$,…,可知分子中a的次数是连续的偶数,分母是连续的奇数,从而可以得到第2016个式子,本题得以解决.
解答 解:∵一组按规律排列的式子:a2,$\frac{{a}^{4}}{3}$,$\frac{{a}^{6}}{5}$,$\frac{{a}^{8}}{7}$,…,
∴第2016个式子是:$\frac{{a}^{2×2016}}{2×2016-1}=\frac{{a}^{4032}}{4031}$,
故选C.
点评 本题考查单项式,解题的关键是发现其中的规律,得到第2016个式子.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.定义三角 表示3abc,方框
表示3abc,方框 表示xz+wy,则
表示xz+wy,则 ×
× 的结果为( )
的结果为( )
 表示3abc,方框
表示3abc,方框 表示xz+wy,则
表示xz+wy,则 ×
× 的结果为( )
的结果为( )| A. | 72m2n-45mn2 | B. | 72m2n+45mn2 | C. | 24m2n-15mn2 | D. | 24m2n+15mn2 |
18. 在△ABC中∠B=30°,AB=4,BC=3,则S△ABC=( )
在△ABC中∠B=30°,AB=4,BC=3,则S△ABC=( )
 在△ABC中∠B=30°,AB=4,BC=3,则S△ABC=( )
在△ABC中∠B=30°,AB=4,BC=3,则S△ABC=( )| A. | 3 | B. | 4 | C. | 1.5 | D. | 2 |
15.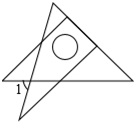 将一副直角三角板如图放置,使含30°角的三角板的直角边和含45°角的三角板的一条直角边重合,则∠1的度数为( )
将一副直角三角板如图放置,使含30°角的三角板的直角边和含45°角的三角板的一条直角边重合,则∠1的度数为( )
 将一副直角三角板如图放置,使含30°角的三角板的直角边和含45°角的三角板的一条直角边重合,则∠1的度数为( )
将一副直角三角板如图放置,使含30°角的三角板的直角边和含45°角的三角板的一条直角边重合,则∠1的度数为( )| A. | 60° | B. | 75° | C. | 65° | D. | 70° |
2.在算式(-2)□(-3)的□中填上运算符号,使结果最小,运算符号是( )
| A. | 加号 | B. | 减号 | C. | 乘号 | D. | 除号 |
12.在式子$\frac{1}{x+1}$,$\frac{1}{x+2}$,$\sqrt{x+1}$,$\sqrt{x+2}$中,x可以同时取-1和-2的是( )
| A. | $\frac{1}{x+1}$ | B. | $\frac{1}{x+2}$ | C. | $\sqrt{x+1}$ | D. | $\sqrt{x+2}$ |
16.在△ABC中,若∠BAC=90°,则( )
| A. | BC=AB+AC | B. | AC2=AB2+BC2 | C. | AB2=AC2+BC2 | D. | BC2=AB2+AC2 |
17.计算$\sqrt{2}$•$\sqrt{5}$的结果是( )
| A. | $\sqrt{7}$ | B. | $\sqrt{10}$ | C. | $\root{4}{10}$ | D. | 10 |
