题目内容
10.在平静的湖面上,有一支红莲,高出水面1米,一阵风吹来,红莲移到一边,花朵齐及水面,已知红莲移动的水平距离为2米,这里的水深为( )米.| A. | 1.5 | B. | 2 | C. | 2.5 | D. | 1 |
分析 设水深为h米,则红莲的高(h+1)米,因风吹花朵齐及水面,且水平距离为2m,那么水深h与水平2米组成一个以(h+1)米为斜边的直角三角形,根据勾股定理即可求出答案.
解答 解:设水深为h米,则红莲的高(h+1)米,且水平距离为2米,
则(h+1)2=22+h2,
解得h=1.5.
故选A.
点评 此题主要考查学生对勾股定理的应用这一知识点的理解和掌握,此题的关键是“水深h与红莲移动的水平距离为2米组成一个以(h+1)米为斜边的直角三角形”这是此题的突破点,此题难度不大,属于中档题.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
20.为了估计池塘两岸A、B间的距离,杨阳在池塘的一侧选取了一点P,测得PA=14m,PB=11m,那么AB间的距离不可能是( )
| A. | 5m | B. | 15m | C. | 20m | D. | 26m |
1. 如图,用火柴棍拼成一排由三角形组成的图形.若拼成的图形中有n个三角形,则需要火柴棍的根数是( )
如图,用火柴棍拼成一排由三角形组成的图形.若拼成的图形中有n个三角形,则需要火柴棍的根数是( )
 如图,用火柴棍拼成一排由三角形组成的图形.若拼成的图形中有n个三角形,则需要火柴棍的根数是( )
如图,用火柴棍拼成一排由三角形组成的图形.若拼成的图形中有n个三角形,则需要火柴棍的根数是( )| A. | n+2 | B. | n+3 | C. | 2n-1 | D. | 2n+1 |
18. 在△ABC中∠B=30°,AB=4,BC=3,则S△ABC=( )
在△ABC中∠B=30°,AB=4,BC=3,则S△ABC=( )
 在△ABC中∠B=30°,AB=4,BC=3,则S△ABC=( )
在△ABC中∠B=30°,AB=4,BC=3,则S△ABC=( )| A. | 3 | B. | 4 | C. | 1.5 | D. | 2 |
5.已知,在△ABC中,AD为BC边上的中线,AC=5,AD=4,则AB的取值范围是( )
| A. | 1<AB<9 | B. | 3<AB<13 | C. | 5<AB<13 | D. | 9<AB<13 |
15.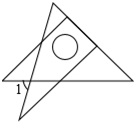 将一副直角三角板如图放置,使含30°角的三角板的直角边和含45°角的三角板的一条直角边重合,则∠1的度数为( )
将一副直角三角板如图放置,使含30°角的三角板的直角边和含45°角的三角板的一条直角边重合,则∠1的度数为( )
 将一副直角三角板如图放置,使含30°角的三角板的直角边和含45°角的三角板的一条直角边重合,则∠1的度数为( )
将一副直角三角板如图放置,使含30°角的三角板的直角边和含45°角的三角板的一条直角边重合,则∠1的度数为( )| A. | 60° | B. | 75° | C. | 65° | D. | 70° |
2.在算式(-2)□(-3)的□中填上运算符号,使结果最小,运算符号是( )
| A. | 加号 | B. | 减号 | C. | 乘号 | D. | 除号 |
20.计算${(-\frac{1}{2}{a^2}b)^3}$的结果正确的是( )
| A. | $\frac{1}{4}{a^4}{b^2}$ | B. | $\frac{1}{8}{a^6}{b^3}$ | C. | $-\frac{1}{8}{a^6}{b^3}$ | D. | $-\frac{1}{8}{a^5}{b^3}$ |
