题目内容

15．若△ABC∽△DEF，△ABC与△DEF的相似比为2：3，则S△DEF：S△ABC为（　　）
A．2：3B．9：4C．4：9D．3：2

分析 根据相似三角形面积的比等于相似比的平方解答．

解答 解：∵△ABC∽△DEF，△ABC与△DEF的相似比为2：3，
∴S△ABC：S△DEF=（$\frac{2}{3}$）2=$\frac{4}{9}$，
S△DEF：S△ABC=9：4，
故选B．

点评 本题考查的是相似三角形的性质，利用相似三角形面积的比等于相似比的平方是解答此题的关键．

练习册系列答案
相关题目
6．先化简，再求值：$\frac{{x}^{2}-2x}{{x}^{2}-4}$÷（x-2-$\frac{2x-4}{x+2}$），其中x=3．
6．在平面直角坐标系中，如果点M（-1，a-1）在第三象限，那么a的取值范围是a＜1．
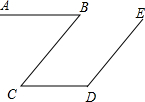3．已知：如图所示，AB∥CD，∠B+∠D=180°．求证：BC∥DE
证明：∵AB∥CD  已知
∴∠B=∠C（两直线平行，内错角相等）
∵∠B+∠D=180°已知
∴∠C+∠D=180°  （等量代换）
∴BC∥DE（同旁内角互补，两直线平行）
10．给出下列命题，其中，真命题的个数是（　　）
①平行四边形的对角线互相平分
②对角线相等的四边形是矩形
③菱形的对角线互相垂直平分
④对角线互相垂直且相等的四边形是正方形．
A．4个B．3个C．2个D．1个
20．完成证明，说明理由．已知：如图，BC∥DE，点E在AB边上，DE、AC交于点F，∠1=∠2，∠3=∠4，求证AE∥CD．
证明：∵BC∥DE（已知），
∴∠4=∠FCB（两直线平行，同位角相等）．
∵∠3=∠4（已知），
∴∠3=∠FCB（等量代换）．
∵∠1=∠2（已知），
∴∠1+∠FCE=∠2+∠FCE（等式的性质）．
即∠FCB=∠ECB，
∴∠3=∠ECD（等量代换）．
∴AE∥CD（内错角相等，两直线平行）．
7．在平面直角坐标系中，点A、B的坐标分别为（a，0），（0，b），其中a，b满足$\sqrt{a-2b-18}$+|2a-5b-30|=0．将点B向右平移26个单位长度得到点C，如图①所示．
（1）求点A，B，C的坐标；
（2）点M，N分别为线段BC，OA上的两个动点，点M从点C向左以1.5个单位长度/秒运动，同时点N从点O向点A以2个单位长度/秒运动，如图②所示，设运动时间为t秒（0＜t＜15）．
①当CM＜AN时，求t的取值范围；
②是否存在一段时间，使得S四边形MNOB＞2S四边形MNAC？若存在，求出t的取值范围；若不存在，说明理由．
4．如图，每个图形都由同样大小的“”按照一定的规律组成，其中第1个图形有1个“”，第2个图形有2个“”，第3个图形有5个“”，…，则第6个图形中“”的个数为（　　）
A．23B．24C．25D．26
5．不等式组$\left\{\begin{array}{l}x-2＞0\\ x-3＜0\end{array}\right.$的解集是（　　）
A．x＞2B．x＜3C．2＜x＜3D．无解

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网