题目内容
7.在平面直角坐标系中,点A、B的坐标分别为(a,0),(0,b),其中a,b满足$\sqrt{a-2b-18}$+|2a-5b-30|=0.将点B向右平移26个单位长度得到点C,如图①所示.(1)求点A,B,C的坐标;
(2)点M,N分别为线段BC,OA上的两个动点,点M从点C向左以1.5个单位长度/秒运动,同时点N从点O向点A以2个单位长度/秒运动,如图②所示,设运动时间为t秒(0<t<15).
①当CM<AN时,求t的取值范围;
②是否存在一段时间,使得S四边形MNOB>2S四边形MNAC?若存在,求出t的取值范围;若不存在,说明理由.

分析 (1)由条件可求得a、b的值,则可求得A、B两点的坐标,再由平移可求得C点坐标;
(2)①用t可分别表示出CM和AN,由条件可得到关于t不等式,可求得t的取值范围;②用t表示出四边形MNOB和四边形MNAC的面积,由条件得到t的不等式,再结合t的取值范围进行判定即可.
解答 解:
(1)∵$\sqrt{a-2b-18}$+|2a-5b-30=0,且$\sqrt{a-2b-18}$≥0,|2a-5b-30|≥0,
∴$\left\{\begin{array}{l}{a-2b-18=0}\\{2a-5b-30=0}\end{array}\right.$,解得:$\left\{\begin{array}{l}{a=30}\\{b=6}\end{array}\right.$,
∴A(30,0),B(0,6),
又∵点C是由点B向右平移26个单位长度得到,
∴C(26,6);
(2)①由(1)可知:OA=30,
∵点M从点C向右以1.5个单位长度/秒运动,点N从点O向点A以2个单位长度/秒运动,
∴CM=1.5t,ON=2t,
∴AN=30-2t
∵CM<AN,
∴1.5t<30-2t,解得t<$\frac{60}{7}$,而0<t<15,
∴0<t<$\frac{60}{7}$;
②由题意可知CM=1.5t,ON=2t,
∴BM=BC-CM=26-1.5t,AN=30-2t,
又B(0,6),
∴OB=6,
∴S四边形MNOB=$\frac{1}{2}$OB(BM+ON)=3(26-1.5t+2t)=3(26+0.5t),S四边形MNAC=$\frac{1}{2}$OB(AN+CM)=3(30-2t+1.5t)=3(30-0.5t),
当S四边形MNOB>2S四边形MNAC时,则有3(26+0.5t)>2×3(30-0.5t),解得t>$\frac{68}{3}$>15,
∴不存在使S四边形MNOB>2S四边形MNAC的时间段.
点评 本题为动态几何问题,涉及知识点有非负数的性质、平移的性质、梯形的面积等.在(1)中求得a、b的值是解题的关键,在(2)中用t表示出相应线段的长度是解题的关键.本题考查知识点相对较少,难度不大.

 阅读快车系列答案
阅读快车系列答案| A. | 2:3 | B. | 9:4 | C. | 4:9 | D. | 3:2 |
 如图,PA和PB是⊙O的切线,点A和B是切点,AC是⊙O的直径,已知∠P=40°,则∠ACB的大小是( )
如图,PA和PB是⊙O的切线,点A和B是切点,AC是⊙O的直径,已知∠P=40°,则∠ACB的大小是( )| A. | 60° | B. | 65° | C. | 70° | D. | 75° |
 在下列软件的图标中,其中是中心对称图形的有( )
在下列软件的图标中,其中是中心对称图形的有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
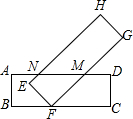 张萌的手中有长方形ABCD(AD∥BC)和长方形EFGH(EH∥FG)两张纸片,她将这两张纸片按如图所示的方式防置,是的FG,EH分别交AD于M,N两点,并测得∠MFC=30°,则∠ANH的度数为( )
张萌的手中有长方形ABCD(AD∥BC)和长方形EFGH(EH∥FG)两张纸片,她将这两张纸片按如图所示的方式防置,是的FG,EH分别交AD于M,N两点,并测得∠MFC=30°,则∠ANH的度数为( )| A. | 120° | B. | 130° | C. | 140° | D. | 150° |
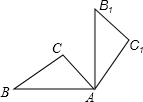 在△ABC中,∠C=90°,BC=4cm,AC=3cm,把△ABC绕点A顺时针旋转90°后,得到△A1B1C1(如图所示),则线段AB所扫过的面积为( )
在△ABC中,∠C=90°,BC=4cm,AC=3cm,把△ABC绕点A顺时针旋转90°后,得到△A1B1C1(如图所示),则线段AB所扫过的面积为( )| A. | 5$\sqrt{2}$ | B. | $\frac{25}{4}$πcm2 | C. | $\frac{25}{2}$πcm2 | D. | 5πcm2 |
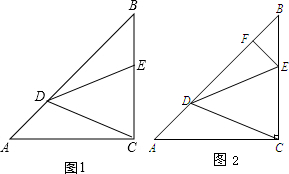 △ABC中,AC=BC,∠ACB=90°,点D,E分别在AB,BC上,且AD=BE,BD=AC.
△ABC中,AC=BC,∠ACB=90°,点D,E分别在AB,BC上,且AD=BE,BD=AC. 如图,△ABC是等边三角形,点P是三角形内的任意一点,PD∥AB,PE∥BC,PF∥AC,若△ABC的周长为12,则PD+PE+PF=( )
如图,△ABC是等边三角形,点P是三角形内的任意一点,PD∥AB,PE∥BC,PF∥AC,若△ABC的周长为12,则PD+PE+PF=( )