题目内容
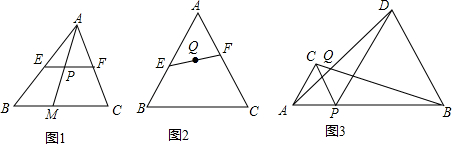
20. 完成证明,说明理由.已知:如图,BC∥DE,点E在AB边上,DE、AC交于点F,∠1=∠2,∠3=∠4,求证AE∥CD.
完成证明,说明理由.已知:如图,BC∥DE,点E在AB边上,DE、AC交于点F,∠1=∠2,∠3=∠4,求证AE∥CD.证明:∵BC∥DE(已知),
∴∠4=∠FCB(两直线平行,同位角相等).
∵∠3=∠4(已知),
∴∠3=∠FCB(等量代换).
∵∠1=∠2(已知),
∴∠1+∠FCE=∠2+∠FCE(等式的性质).
即∠FCB=∠ECB,
∴∠3=∠ECD(等量代换).
∴AE∥CD(内错角相等,两直线平行).
分析 先用平行线得到∠4=∠FCB,再用等式性质,最后用平行线的判定即可.
解答 证明:∵BC∥DE(已知),
∴∠4=∠FCB(两直线平行,同位角相等).
∵∠3=∠4(已知),
∴∠3=∠FCB(等量代换).
∵∠1=∠2(已知),
∴∠1+∠FCE=∠2+∠FCE(等式的性质).
即∠FCB=∠ECD,
∴∠3=∠ECD(等量代换).
∴AE∥CD(内错角相等,两直线平行).
故答案为:∠FCB,两直线平行,同位角相等,∠FCB,等量代换,等式的性质,∠ECD,等量代换,内错角相等,两直线平行.
点评 此题是平行线的性质是判定,还用到等式的性质,解本题关键是熟练运用平行线的性质和判定.一道中考常考题.

练习册系列答案
相关题目
11.下列命题中,是真命题的是( )
| A. | 有理数都是有限小数 | |
| B. | 同旁内角互补 | |
| C. | 函数y=$\frac{1}{\sqrt{x-3}}$自变量x的取值范围是x≥3 | |
| D. | 若甲、乙两组数据中各有20个数据,平均数$\overline{{x}_{甲}}$=$\overline{{x}_{乙}}$,方差S甲2=1.25,S乙2=0.96,则说明乙组数据比甲组数据稳定 |
8.若一次函数y=(m-3)x+5的函数值,y随x的增大而增大,则( )
| A. | m<0 | B. | m>0 | C. | m<3 | D. | m>3 |
15.若△ABC∽△DEF,△ABC与△DEF的相似比为2:3,则S△DEF:S△ABC为( )
| A. | 2:3 | B. | 9:4 | C. | 4:9 | D. | 3:2 |
5. 如图,已知AE=CF,∠AFD=∠CEB,添加一个条件后,仍无法判定△ADF≌△CBE的是( )
如图,已知AE=CF,∠AFD=∠CEB,添加一个条件后,仍无法判定△ADF≌△CBE的是( )
 如图,已知AE=CF,∠AFD=∠CEB,添加一个条件后,仍无法判定△ADF≌△CBE的是( )
如图,已知AE=CF,∠AFD=∠CEB,添加一个条件后,仍无法判定△ADF≌△CBE的是( )| A. | ∠A=∠C | B. | AD=CB | C. | BE=DF | D. | AD∥BC |
12. 在下列软件的图标中,其中是中心对称图形的有( )
在下列软件的图标中,其中是中心对称图形的有( )
 在下列软件的图标中,其中是中心对称图形的有( )
在下列软件的图标中,其中是中心对称图形的有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
9.函数y=$\frac{x}{3-x}$的自变量取值范围是( )
| A. | x≠3 | B. | x≠0 | C. | x≠3且x≠0 | D. | x<3 |
 如图,已知直线y=-x+3与x轴、y轴分别交于A,B两点,抛物线y=-x2+bx+c经过A,B两点,点P在线段OA上,从点O出发,向点A以1个单位/秒的速度匀速运动;同时,点Q在线段AB上,从点A出发,向点B以$\sqrt{2}$个单位/秒的速度匀速运动,连接PQ,设运动时间为t秒.
如图,已知直线y=-x+3与x轴、y轴分别交于A,B两点,抛物线y=-x2+bx+c经过A,B两点,点P在线段OA上,从点O出发,向点A以1个单位/秒的速度匀速运动;同时,点Q在线段AB上,从点A出发,向点B以$\sqrt{2}$个单位/秒的速度匀速运动,连接PQ,设运动时间为t秒.