题目内容
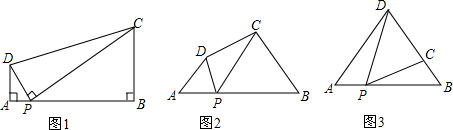
2.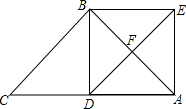 如图,已知:在△ABC中,∠ABC=90°,AB=BC=2,D是边AC上一点(D与A,C不重合),过点A作AE垂直AC,且满足AE=CD.交边AB于点F.
如图,已知:在△ABC中,∠ABC=90°,AB=BC=2,D是边AC上一点(D与A,C不重合),过点A作AE垂直AC,且满足AE=CD.交边AB于点F.(1)试判断△DBE的形状,并证明你的结论;
(2)当点D在边AC上运动时,四边形ADBE的面积是否发生变化?若不变,求出四边形ADBE的面积;若改变,请说明理由;
(3)当△BDF是等腰三角形时,请直接写出AD的长.
分析 (1)根据在△ABC中,∠ABC=90°,AB=BC=2可得出∠CAB=∠ACB=45°,再由AE⊥AC可得出∠EAC=90°,故可得出∠BAE=45°,由SAS定理可得出△CBD≌△ABE,故可得出BD=BE,由此可得出结论;
(2)根据(1)中△CBD≌△ABE可知四边形ADBE的面积不变,再由三角形的面积公式即可得出结论;
(3)分两种情况分别讨论即可求得.
解答 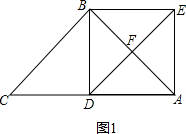 解:(1)△DBE是等腰直角三角形.
解:(1)△DBE是等腰直角三角形.
理由:如图1,∵∠ABC=90°,AB=BC=2,
∴∠CAB=∠ACB=45°.
∵AE⊥AC,
∴∠EAC=90°,
∴∠BAE=45°.
在△CBD与△ABE中,
∵$\left\{\begin{array}{l}BC=AB\\∠C=∠BAE\\ CD=AE\end{array}\right.$,
∴△CBD≌△ABE(SAS),
∴BD=BE,∠CBD=∠ABE,
∵∠CBD+∠ABD=90°,
∴∠ABE+∠ABD=90°,
即∠BDE=90°,
即△DBE是等腰直角三角形;
(2)不变.
∵由(1)知△CBD≌△ABE,
∴S四边形ADBE=S△ABC=$\frac{1}{2}$×2×2=2;
(3)当BF=DF时,则∠BDE=∠FBD,如图1,
∵△DBE是等腰直角三角形,
∴∠BDE=45°,
∴∠FBD=45°
∴∠CBD=45°,
∴∠CBD=∠ABD,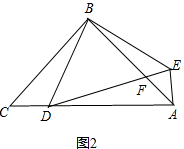
∴AD=CD,
∴AD=$\frac{1}{2}$AC,
∵AB=BC=2,
∴AC=2$\sqrt{2}$,
∴AD=$\sqrt{2}$;
当BD=DF时,如图2,
∵△ABC是等腰直角三角形,△BDE是等腰直角三角形,
∴∠C=∠CAB=45°,∠BDE=∠BED=45°,
∴∠C=∠BDE,
∵∠ADB=∠C+∠CBD=∠BDE+∠FDA,
∴∠CDB=∠ADF,
在△BCD和△DAF中
$\left\{\begin{array}{l}{∠C=∠DAF=45°}\\{∠CBD=∠ADF}\\{BD=DF}\end{array}\right.$
∴△BCD≌△DAF(AAS),
∴AD=BC=2.
∴当△BDF是等腰三角形时,AD的长为$\sqrt{2}$或2.
点评 本题是四边形的综合题,考查了等腰直角三角形的判定和性质,三角形全等的判定和性质,等腰三角形的性质,熟练掌握性质定理是解题的关键

 名校通行证有效作业系列答案
名校通行证有效作业系列答案| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
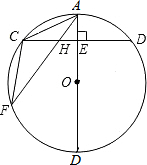 如图,AB为⊙O的直径,弦CD⊥AB于点E,点F是⊙O上一点,连接AC、AF、CF,求证:△ACH∽△AFC.
如图,AB为⊙O的直径,弦CD⊥AB于点E,点F是⊙O上一点,连接AC、AF、CF,求证:△ACH∽△AFC.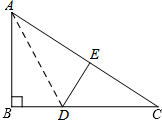 如图,在Rt△ABC中,∠ABC=90°,AC=10,BC=8,AD是∠BAC的平分线,点E是斜边AC上的一点,且AE=AB,沿△DEC的一个内角平分线折叠,使点C落在DE所在直线上,则折痕的长度为$\frac{12\sqrt{2}}{7}$和$\frac{3\sqrt{5}}{2}$.
如图,在Rt△ABC中,∠ABC=90°,AC=10,BC=8,AD是∠BAC的平分线,点E是斜边AC上的一点,且AE=AB,沿△DEC的一个内角平分线折叠,使点C落在DE所在直线上,则折痕的长度为$\frac{12\sqrt{2}}{7}$和$\frac{3\sqrt{5}}{2}$.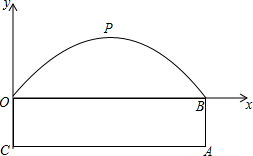 如图所示,某隧道横截面的轮廓线由抛物线对称的一部分和矩形的一部分组成,最大高度为6米,底部宽度为12米,OC=3米,现如图建立平面直角坐标系.
如图所示,某隧道横截面的轮廓线由抛物线对称的一部分和矩形的一部分组成,最大高度为6米,底部宽度为12米,OC=3米,现如图建立平面直角坐标系.