题目内容
17.对角线长为2$\sqrt{2}$的正方形的边长为2.分析 设正方形的边长为x,利用正方形的性质和勾股定理得出方程,解方程即可.
解答 解:设正方形的边长为x,由勾股定理得:
∴x2+x2=(2$\sqrt{2}$)2,
解得:x=±2(负值舍去),
即正方形的边长为2,
故答案为:2.
点评 此题主要考查了正方形的性质、勾股定理;熟练掌握正方形的性质,应用勾股定理是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.把方程3x2=5x+2化为一元二次方程的一般形式是( )
| A. | 3x2-5x=2 | B. | 3x2-2=5x | C. | 3x2-5x-2=0 | D. | x2-x-2=0 |

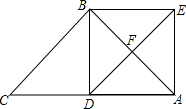 如图,已知:在△ABC中,∠ABC=90°,AB=BC=2,D是边AC上一点(D与A,C不重合),过点A作AE垂直AC,且满足AE=CD.交边AB于点F.
如图,已知:在△ABC中,∠ABC=90°,AB=BC=2,D是边AC上一点(D与A,C不重合),过点A作AE垂直AC,且满足AE=CD.交边AB于点F. 如图,抛物线y=ax2-x-$\frac{3}{2}$与x轴正半轴交于点A(3,0).以OA为边在x轴上方作正方形OABC,延长CB交抛物线于点D,再以BD为边向上作正方形BDEF,点E的坐标是($\sqrt{10}+1$,$\sqrt{10}+1$).
如图,抛物线y=ax2-x-$\frac{3}{2}$与x轴正半轴交于点A(3,0).以OA为边在x轴上方作正方形OABC,延长CB交抛物线于点D,再以BD为边向上作正方形BDEF,点E的坐标是($\sqrt{10}+1$,$\sqrt{10}+1$).