题目内容
2.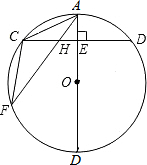 如图,AB为⊙O的直径,弦CD⊥AB于点E,点F是⊙O上一点,连接AC、AF、CF,求证:△ACH∽△AFC.
如图,AB为⊙O的直径,弦CD⊥AB于点E,点F是⊙O上一点,连接AC、AF、CF,求证:△ACH∽△AFC.
分析 由垂径定理得出$\widehat{AD}=\widehat{AC}$,由圆周角定理得出∠ACH=∠AFC,再由公共角∠CAH=∠FAC,即可得出结论.
解答 证明:∵AB为⊙O的直径,弦CD⊥AB,
∴$\widehat{AD}=\widehat{AC}$,
∴∠ACH=∠AFC,
又∵∠CAH=∠FAC,
∴△ACH∽△AFC.
点评 本题考查了相似三角形的判定与性质、垂径定理、圆周角定理;熟练掌握相似三角形的判定方法,由圆周角定理得出角相等是解题的关键.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
13. 如图,两个同心圆的半径分别为3cm和5cm,大圆的一条弦AB与小圆相切,则弦AB的长为( )
如图,两个同心圆的半径分别为3cm和5cm,大圆的一条弦AB与小圆相切,则弦AB的长为( )
 如图,两个同心圆的半径分别为3cm和5cm,大圆的一条弦AB与小圆相切,则弦AB的长为( )
如图,两个同心圆的半径分别为3cm和5cm,大圆的一条弦AB与小圆相切,则弦AB的长为( )| A. | 3cm | B. | 4cm | C. | 6cm | D. | 8cm |

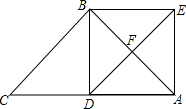 如图,已知:在△ABC中,∠ABC=90°,AB=BC=2,D是边AC上一点(D与A,C不重合),过点A作AE垂直AC,且满足AE=CD.交边AB于点F.
如图,已知:在△ABC中,∠ABC=90°,AB=BC=2,D是边AC上一点(D与A,C不重合),过点A作AE垂直AC,且满足AE=CD.交边AB于点F.