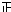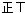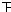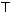题目内容
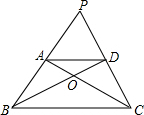如图，梯形ABCD中，AD∥BC，对角线AC和BD交于点O，延长BA和CD交于点P，已知△PAD和△ODC的面积分别为20和6，则△PBC的面积为（ ）| A、40 | B、42 | C、45 | D、48 |
考点：相似三角形的判定与性质
专题：
分析：如图，证明S△ABO=S△CDO=6；设S△ADO=λ，S△BCO=μ；证明λμ=36③；证明
=
④，联立③④，求出λ、μ即可解决问题．
| 20 |
| 20+λ+μ+12 |
| λ2 |
| 36 |
解答：解：∵AD∥BC，
∴S△ABD=S△ADC，
∴S△ABO=S△CDO=6；
设S△ADO=λ，S△BCO=μ；
则
=
，即
=
①；
∵AD∥BC，
∴△ADO∽△BCO，
∴
=(
)2，即
=(
)2②，
由①②得：λμ=36③；
∵AD∥BC，
∴△PAD∽△PBC，
∴
=(
)2，而
=
，
∴
=
④，
联立③、④并解得：λ=4，μ=9，
∴△PBC的面积=45，
故选C．
解：∵AD∥BC，∴S△ABD=S△ADC，
∴S△ABO=S△CDO=6；
设S△ADO=λ，S△BCO=μ；
则
| S△ADO |
| S△BCO |
| AO |
| CO |
| λ |
| 6 |
| AO |
| CO |
∵AD∥BC，
∴△ADO∽△BCO，
∴
| S△ADO |
| S△BCO |
| AO |
| CO |
| λ |
| μ |
| AO |
| CO |
由①②得：λμ=36③；
∵AD∥BC，
∴△PAD∽△PBC，
∴
| S△PAD |
| S△PBC |
| AD |
| BC |
| AD |
| BC |
| AO |
| CO |
∴
| 20 |
| 20+λ+μ+12 |
| λ2 |
| 36 |
联立③、④并解得：λ=4，μ=9，
∴△PBC的面积=45，
故选C．
点评：该题主要考查了相似三角形的判定及其性质的应用问题；牢固掌握相似三角形的判定及其性质定理的内容是灵活运用、解题的基础和关键．
练习册系列答案
轻松夺冠全能掌控卷系列答案
相关题目
已知函数y=（x-1）2-1，当函数值y随x的增大而减小时，x的取值范围是（ ）
| A、x＜0 | B、x＞0 |
| C、x＜1 | D、x＞1 |
小彬的爸爸制作了一件边框为长方形的工艺品，挂在墙上很漂亮，但小彬看来看去总觉得它不像长方形，经过思考小彬仅用一把刻度尺（尺的长度足够）就解决了问题，你能说出他用的是什么方法吗？（简要说明一下操作过程及相关理由）某商店卖出两件衣服，每件60元，其中一件赚20%，另一件亏20%，那么这两件衣服卖出后，商店（ ）
| A、不赚不亏 | B、赚5元 |
| C、亏5元 | D、赚10元 |
已知命题A：“关于x的一元二次方程x2-2ax+1=0一定有实根”．在下列选项中，可以作为“命题A是假命题”的反例的是（ ）
| A、a=-3 | B、a=-1 |
| C、a=0 | D、a=2 |