题目内容
是否存在整数k,使关于x的分式方程
-
=
的解大于-2且小于2?若存在,请求出;若不存在,请说理由.
| k-1 |
| x2-1 |
| k-2 |
| x2+x |
| 1 |
| x-x2 |
考点:分式方程的解
专题:
分析:先求出分式方程的解为x=
,再根据解大于-2且小于2得出不等式组-2<
<2,解不等式组求出-3<k<5,然后根据k为整数及最简公分母不为0即可求解.
| -k+1 |
| 2 |
| -k+1 |
| 2 |
解答:解:方程两边都乘x(x+1)(x-1)得,
x(k-1)-(x-1)(k-2)=-(x+1),
整理得,2x=-k+1,
解得x=
.
∵关于x的分式方程
-
=
的解大于-2且小于2,
∴-2<
<2,
∴-3<k<5,
∵k为整数,
∴k=-2,-1,0,1,2,3,4.
∵x(x+1)(x-1)≠0,
∴x≠0,1,-1,
∴
≠0,1,-1,
∴k≠1,-1,3,
∴k=-2,0,2,4.
x(k-1)-(x-1)(k-2)=-(x+1),
整理得,2x=-k+1,
解得x=
| -k+1 |
| 2 |
∵关于x的分式方程
| k-1 |
| x2-1 |
| k-2 |
| x2+x |
| 1 |
| x-x2 |
∴-2<
| -k+1 |
| 2 |
∴-3<k<5,
∵k为整数,
∴k=-2,-1,0,1,2,3,4.
∵x(x+1)(x-1)≠0,
∴x≠0,1,-1,
∴
| -k+1 |
| 2 |
∴k≠1,-1,3,
∴k=-2,0,2,4.
点评:本题考查了分式方程的解,一元一次不等式组的解法,正确求出分式方程的解是解题的关键,理解分式方程产生增根的原因进而去掉使最简公分母为0的k值是本题的难点.

练习册系列答案
相关题目
 如图,抛物线y1=a(x+2)2-3与y2=
如图,抛物线y1=a(x+2)2-3与y2=| 1 |
| 2 |
①无论x取何值,y2总是正数;②a=1;③2AB=3AC;④当x=0时,y1>y2.
| A、①② | B、①③ | C、③④ | D、①④ |
 如图,P为⊙O外一点,PA,PB分别切⊙O于A,B,CD切⊙O于点E,分别交PA,PB于点C,D.若PA=5,则△PCD的周长和∠COD分别为( )
如图,P为⊙O外一点,PA,PB分别切⊙O于A,B,CD切⊙O于点E,分别交PA,PB于点C,D.若PA=5,则△PCD的周长和∠COD分别为( )A、5,
| ||
B、7,90°+
| ||
C、10,90°-
| ||
D、10,90°+
|
若
=
,则
=( )
| m+n |
| m-n |
| 7 |
| 3 |
| m |
| m-n |
A、
| ||
B、
| ||
C、
| ||
D、
|
 如图,AB∥CD,直线PQ分别交AB、CD于点F、E,EG是∠FED的平分线,交AB于点G.若∠QED=40°,那么∠FEG等于
如图,AB∥CD,直线PQ分别交AB、CD于点F、E,EG是∠FED的平分线,交AB于点G.若∠QED=40°,那么∠FEG等于 小亮家想利用房屋侧面的一面墙,再砌三面墙,围成一个矩形猪圈,如图所示,在平行墙的一边开一个1米宽的小门.现在已备足可以砌11米长的墙的材料.
小亮家想利用房屋侧面的一面墙,再砌三面墙,围成一个矩形猪圈,如图所示,在平行墙的一边开一个1米宽的小门.现在已备足可以砌11米长的墙的材料.
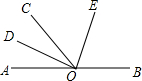 如图,O为直线AB上一点,OD平分∠AOC,∠DOE=90°.
如图,O为直线AB上一点,OD平分∠AOC,∠DOE=90°.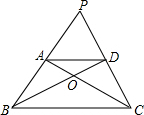 如图,梯形ABCD中,AD∥BC,对角线AC和BD交于点O,延长BA和CD交于点P,已知△PAD和△ODC的面积分别为20和6,则△PBC的面积为( )
如图,梯形ABCD中,AD∥BC,对角线AC和BD交于点O,延长BA和CD交于点P,已知△PAD和△ODC的面积分别为20和6,则△PBC的面积为( )