题目内容
如图，在正方形ABCD中，AB=4，AE=2，DF=1，请你判定△BEF的形状，并说明理由．考点：勾股定理的逆定理,勾股定理,正方形的性质
专题：
分析：根据勾股定理求出BE2、EF2、BF2，根据勾股定理的逆定理判断即可．
解答：解：∵△BEF是直角三角形，
理由是：∵在正方形ABCD中，AB=4，AE=2，DF=1，
∴∠A=∠C=∠D=90°，AB=AD=DC=BC=4，DE=4-2=2，CF=4-1=3，
∵由勾股定理得：BE2=AB2+AE2=42+22=20，EF2=DE2+DF2=22+12=5，BF2=BC2+CF2=42+32=25，
∴BE2+EF2=BF2，
∴∠BEF=90°，
即△BEF是直角三角形．
理由是：∵在正方形ABCD中，AB=4，AE=2，DF=1，
∴∠A=∠C=∠D=90°，AB=AD=DC=BC=4，DE=4-2=2，CF=4-1=3，
∵由勾股定理得：BE2=AB2+AE2=42+22=20，EF2=DE2+DF2=22+12=5，BF2=BC2+CF2=42+32=25，
∴BE2+EF2=BF2，
∴∠BEF=90°，
即△BEF是直角三角形．
点评：本题考查了正方形性质，勾股定理，勾股定理的逆定理的应用，解此题的关键是求出BE2+EF2=BF2，注意：一个三角形的两边a、b的平方和等于第三边c的平方，那么这个三角形是直角三角形，难度适中．
练习册系列答案
相关题目
将两个完全相同的长方形拼成如图的图形，长方形的长为a，宽为b，对角线长为c，请你用该图验证勾股定理．
如图所示，在平行四边形ABCD中，E为边AB的中点，AC、DE相交于点O，已知△OAE的面积为1cm2，那么平行四边形ABCD的面积为
如图，在△ABC中，∠ABC=90°，AB=8cm，BC=15cm，P是到△ABC三边距离相等的点，求点P到△ABC三边的距离．顶点是（-2，1），开口方向，形状与抛物线y=
x2相同的抛物线是（ ）
| 1 |
| 2 |
A、y=
| ||
B、y=
| ||
C、y=
| ||
D、y=-
|
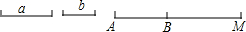阅读：在用尺规作线段AB等于线段a时，小明的具体作法如下：