题目内容
6.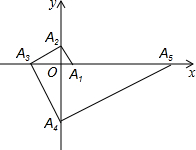 如图,点A1的坐标为(1,0),A2在y轴的正半轴上,且∠A1A2O=30°,过点A2作A2A3⊥A1A2,垂足为A2,交x轴于点A3,过点A3作A3A4⊥A2A3,垂足为A3,交y轴于点A4;过点A4作A4A5⊥A3A4,垂足为A4,交x轴于点A5;过点A5作A5A6⊥A4A5,垂足为A5,交y轴于点A6;…按此规律进行下去,则点A2017的横坐标为31008.
如图,点A1的坐标为(1,0),A2在y轴的正半轴上,且∠A1A2O=30°,过点A2作A2A3⊥A1A2,垂足为A2,交x轴于点A3,过点A3作A3A4⊥A2A3,垂足为A3,交y轴于点A4;过点A4作A4A5⊥A3A4,垂足为A4,交x轴于点A5;过点A5作A5A6⊥A4A5,垂足为A5,交y轴于点A6;…按此规律进行下去,则点A2017的横坐标为31008.
分析 由∠A1A2O=30°结合点A1的坐标即可得出点A2的坐标,由A2A3⊥A1A2结合点A2的坐标即可得出点A3的坐标,同理找出点A4、A5、A6、…的坐标,根据坐标的变化找出变化规律“A4n+1($(\sqrt{3})^{4n}$,0),A4n+2(0,$(\sqrt{3})^{4n+1}$),A4n+3(-$(\sqrt{3})^{4n+2}$,0),A4n+4(0,-$(\sqrt{3})^{4n+3}$)(n为自然数)”,依此规律结合2017=504×4+1即可得出点A2017的坐标,此题得解.
解答 解:∵∠A1A2O=30°,点A1的坐标为(1,0),
∴点A2的坐标为(0,$\sqrt{3}$).
∵A2A3⊥A1A2,
∴点A3的坐标为(-3,0).
同理可得:A4(0,-3$\sqrt{3}$),A5(9,0),A6(0,9$\sqrt{3}$),…,
∴A4n+1($(\sqrt{3})^{4n}$,0),A4n+2(0,$(\sqrt{3})^{4n+1}$),A4n+3(-$(\sqrt{3})^{4n+2}$,0),A4n+4(0,-$(\sqrt{3})^{4n+3}$)(n为自然数).
∵2017=504×4+1,
∴A2017($(\sqrt{3})^{2016}$,0),即(31008,0).
故答案为:31008.
点评 本题考查了规律型中点的坐标以及含30度角的直角三角形,根据点的变化找出变化规律“A4n+1($(\sqrt{3})^{4n}$,0),A4n+2(0,$(\sqrt{3})^{4n+1}$),A4n+3(-$(\sqrt{3})^{4n+2}$,0),A4n+4(0,-$(\sqrt{3})^{4n+3}$)(n为自然数)”是解题的关键.

 快捷英语周周练系列答案
快捷英语周周练系列答案| A. | 2 | B. | $\sqrt{2}$ | C. | 2$\sqrt{2}$ | D. | 4 |
| A. | (π-3.14)0=0 | B. | (-2x+y)(2x+y)=y2-4x2 | ||
| C. | (-2x2y)3=-6x6y3 | D. | 5a2-a2=4 |
| A. | -5 | B. | 5 | C. | 13 | D. | 15 |
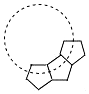 如图,用若干个全等的正五边形可以拼成一个环状,如图是前3个正五边形的拼接情况,要完全拼成一个圆环还需要的正五边形个数是7.
如图,用若干个全等的正五边形可以拼成一个环状,如图是前3个正五边形的拼接情况,要完全拼成一个圆环还需要的正五边形个数是7. 如图,在平面直角坐标系xOy中,点A的坐标是(2,0),点B的坐标是(0,4),点C在x轴上运动(不与点A重合),点D在y轴上运动(不与点B重合),当点C的坐标为(-4,0)、(-2,0)、(4,0)时,以点C、O、D为顶点的三角形与△AOB全等.
如图,在平面直角坐标系xOy中,点A的坐标是(2,0),点B的坐标是(0,4),点C在x轴上运动(不与点A重合),点D在y轴上运动(不与点B重合),当点C的坐标为(-4,0)、(-2,0)、(4,0)时,以点C、O、D为顶点的三角形与△AOB全等.