题目内容
15．已知一个正六边形的边心距为$\sqrt{3}$，则它的半径为2．分析 设正六边形的中心是O，一边是AB，过O作OG⊥AB与G，在直角△OAG中，根据三角函数即可求得OA．
解答 
解：如图，在Rt△AOG中，OG=$\sqrt{3}$，∠AOG=30°，
∴OA=OG÷cos 30°=$\sqrt{3}$÷$\frac{\sqrt{3}}{2}$=2；
故答案为：2．
点评 本题主要考查正多边形的计算问题，常用的思路是转化为直角三角形中边和角的计算，属于常规题．
练习册系列答案
相关题目
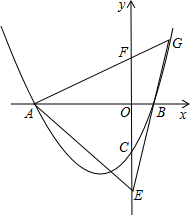已知抛物线y=$\frac{1}{2}{x}^{2}+2mx-4m-2$（m≥0）与x轴交于A、B两点，A点在B点的左边．与y轴交于点C．
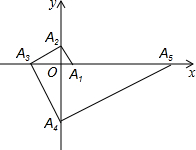如图，点A1的坐标为（1，0），A2在y轴的正半轴上，且∠A1A2O=30°，过点A2作A2A3⊥A1A2，垂足为A2，交x轴于点A3，过点A3作A3A4⊥A2A3，垂足为A3，交y轴于点A4；过点A4作A4A5⊥A3A4，垂足为A4，交x轴于点A5；过点A5作A5A6⊥A4A5，垂足为A5，交y轴于点A6；…按此规律进行下去，则点A2017的横坐标为31008．
如图，以点O为位似中心，将△ABC放大得到△DEF，若AD=OA，△ABC的面积为4，则△DEF的面积为（ ）
20．下列说法中错误的是（ ）
| A． | “任意画一个五边形，其内角和为540°”是必然事件 | |
| B． | “投掷一枚均匀的硬币100次，正面朝上50次”是随机事件 | |
| C． | 甲、乙两人在相同条件下各射击10次，他们的成绩平均数相同，方差分别是S甲2=0.4、S乙2=0.6，则甲的射击成绩较稳定 | |
| D． | 了解某村60岁以上老年人的身体健康状况，宜采用抽样方式调查 |
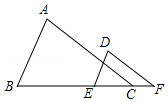如图，已知点B、E、C、F在同一条直线上，∠A=∠D，要使△ABC∽△DEF，还需添加一个条件，你添加的条件是∠B=∠DEC．（只需写一个条件，不添加辅助线和字母）
4．
如图，抛物线y=ax2+bx+c（a≠0）与x轴一个交点为（-2，0），对称轴为直线x=1，则y＜0时x的范围是（ ）
如图，抛物线y=ax2+bx+c（a≠0）与x轴一个交点为（-2，0），对称轴为直线x=1，则y＜0时x的范围是（ ）| A． | x＞4或x＜-2 | B． | -2＜x＜4 | C． | -2＜x＜3 | D． | 0＜x＜3 |
5．实数$\sqrt{9}$的值是（ ）
| A． | 3 | B． | -3 | C． | ±3 | D． | ±9 |