题目内容
17．
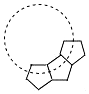如图，用若干个全等的正五边形可以拼成一个环状，如图是前3个正五边形的拼接情况，要完全拼成一个圆环还需要的正五边形个数是7．
分析 设要完全拼成一个圆环需要的正五边形为n个，则围成的多边形为正n边形，利用正五边形的内角计算出正n边的每个内角的度数，然后根据内角和定理得到（n-2）•180°=（360°-2×108°）n，再解方程求出x即可．
解答 解：设要完全拼成一个圆环需要的正五边形为n个，
所以（n-2）•180°=（360°-2×108°）n，解得n=10，
所以要完全拼成一个圆环还需要的正五边形的个数为7．
故答案为7．
点评 本题考查了多边形的内角与外角：多边形内角和定理：（n-2）•180 （n≥3）且n为整数）；外角和为360°．
练习册系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
相关题目
8．
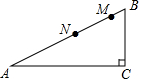如图，∠C=90°，AC=12，CB=5，AM=AC，BN=BC，则MN的长是（ ）
如图，∠C=90°，AC=12，CB=5，AM=AC，BN=BC，则MN的长是（ ）| A． | 2 | B． | 2.6 | C． | 3 | D． | 4 |
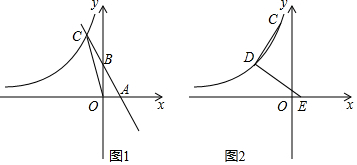
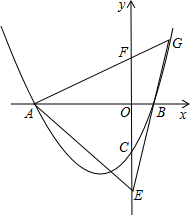已知抛物线y=$\frac{1}{2}{x}^{2}+2mx-4m-2$（m≥0）与x轴交于A、B两点，A点在B点的左边．与y轴交于点C．
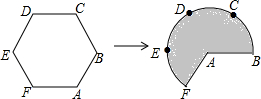如图，将边长为3的正六边形铁丝框ABCDEF变形为以点A为圆心，AB为半径的扇形（忽略铁丝的粗细）．则所得扇形AFB（阴影部分）的面积为（ ）
2．当a，b互为相反数时，代数式a2+ab-4的值为（ ）
| A． | 4 | B． | 0 | C． | -3 | D． | -4 |
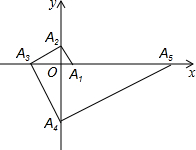如图，点A1的坐标为（1，0），A2在y轴的正半轴上，且∠A1A2O=30°，过点A2作A2A3⊥A1A2，垂足为A2，交x轴于点A3，过点A3作A3A4⊥A2A3，垂足为A3，交y轴于点A4；过点A4作A4A5⊥A3A4，垂足为A4，交x轴于点A5；过点A5作A5A6⊥A4A5，垂足为A5，交y轴于点A6；…按此规律进行下去，则点A2017的横坐标为31008．
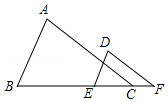如图，已知点B、E、C、F在同一条直线上，∠A=∠D，要使△ABC∽△DEF，还需添加一个条件，你添加的条件是∠B=∠DEC．（只需写一个条件，不添加辅助线和字母）