题目内容
11. 如图,在平面直角坐标系xOy中,点A的坐标是(2,0),点B的坐标是(0,4),点C在x轴上运动(不与点A重合),点D在y轴上运动(不与点B重合),当点C的坐标为(-4,0)、(-2,0)、(4,0)时,以点C、O、D为顶点的三角形与△AOB全等.
如图,在平面直角坐标系xOy中,点A的坐标是(2,0),点B的坐标是(0,4),点C在x轴上运动(不与点A重合),点D在y轴上运动(不与点B重合),当点C的坐标为(-4,0)、(-2,0)、(4,0)时,以点C、O、D为顶点的三角形与△AOB全等.
分析 分三种情况讨论:①当点C在x轴负半轴上,点D在y轴负半轴上时,△AOB≌△COD,②当点C在x轴负半轴上,点D在y轴上时,△AOB≌△DOC,③当点C在x轴的正半轴上,点D在y轴上时,△AOB≌△DOC,分别根据全等三角形的对应边相等,即可得到点C的坐标.
解答 解:如图所示,当点C在x轴负半轴上,点D在y轴负半轴上时,△AOB≌△COD,
∴CO=AO=2,
∴C(-2,0);
如图所示,当点C在x轴负半轴上,点D在y轴上时,△AOB≌△DOC,
∴CO=BO=4,
∴C(-4,0);
如图所示,当点C在x轴的正半轴上,点D在y轴上时,△AOB≌△DOC,
∴CO=BO=4,
∴C(4,0).
故答案为:(-4,0)、(-2,0)、(4,0).
点评 本题主要考查了全等三角形的判定以及坐标与图形性质,解决问题的关键是依据点C的不同位置进行分类讨论.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
2.当a,b互为相反数时,代数式a2+ab-4的值为( )
| A. | 4 | B. | 0 | C. | -3 | D. | -4 |
16.安徽省,政府工作报告》指出,2017年全年将实施亿元以上技改项目1000项,完成投资6600亿元,把6600亿用科学记数法可表示为( )
| A. | 6.6×103 | B. | 66×1010 | C. | 6.600×1011 | D. | 0.66×1012 |
20.下列说法中错误的是( )
| A. | “任意画一个五边形,其内角和为540°”是必然事件 | |
| B. | “投掷一枚均匀的硬币100次,正面朝上50次”是随机事件 | |
| C. | 甲、乙两人在相同条件下各射击10次,他们的成绩平均数相同,方差分别是S甲2=0.4、S乙2=0.6,则甲的射击成绩较稳定 | |
| D. | 了解某村60岁以上老年人的身体健康状况,宜采用抽样方式调查 |
1. 某中学在安全工作月中,进行了“防自然灾害-地震知识知多少”专题调查活动,采取随机抽样的方式进行问卷调查,问卷调查的结果分为“非常了解”、“比较了解”、“基本了解”、“不太了解”四个等级,花粉等级后的数据整理如下表:
某中学在安全工作月中,进行了“防自然灾害-地震知识知多少”专题调查活动,采取随机抽样的方式进行问卷调查,问卷调查的结果分为“非常了解”、“比较了解”、“基本了解”、“不太了解”四个等级,花粉等级后的数据整理如下表:
(1)表中m的值为0.6,n的值为36;
(2)根据表中的数据,请你计算“非常了解”的频率在如图中对应的扇形的圆心角的度数,并补全扇形统计图;
(3)若校一共有2400名学生,请根据调查结果估计全校学生中“比较了解”的人数为多少?
 某中学在安全工作月中,进行了“防自然灾害-地震知识知多少”专题调查活动,采取随机抽样的方式进行问卷调查,问卷调查的结果分为“非常了解”、“比较了解”、“基本了解”、“不太了解”四个等级,花粉等级后的数据整理如下表:
某中学在安全工作月中,进行了“防自然灾害-地震知识知多少”专题调查活动,采取随机抽样的方式进行问卷调查,问卷调查的结果分为“非常了解”、“比较了解”、“基本了解”、“不太了解”四个等级,花粉等级后的数据整理如下表:| 等级 | 非常了解 | 比较了解 | 基本了解 | 不太了解 |
| 频数 | 40 | 120 | n | 4 |
| 频率 | 0.2 | m | 0.18 | 0.02 |
(2)根据表中的数据,请你计算“非常了解”的频率在如图中对应的扇形的圆心角的度数,并补全扇形统计图;
(3)若校一共有2400名学生,请根据调查结果估计全校学生中“比较了解”的人数为多少?
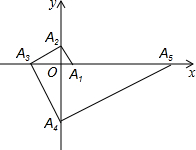 如图,点A1的坐标为(1,0),A2在y轴的正半轴上,且∠A1A2O=30°,过点A2作A2A3⊥A1A2,垂足为A2,交x轴于点A3,过点A3作A3A4⊥A2A3,垂足为A3,交y轴于点A4;过点A4作A4A5⊥A3A4,垂足为A4,交x轴于点A5;过点A5作A5A6⊥A4A5,垂足为A5,交y轴于点A6;…按此规律进行下去,则点A2017的横坐标为31008.
如图,点A1的坐标为(1,0),A2在y轴的正半轴上,且∠A1A2O=30°,过点A2作A2A3⊥A1A2,垂足为A2,交x轴于点A3,过点A3作A3A4⊥A2A3,垂足为A3,交y轴于点A4;过点A4作A4A5⊥A3A4,垂足为A4,交x轴于点A5;过点A5作A5A6⊥A4A5,垂足为A5,交y轴于点A6;…按此规律进行下去,则点A2017的横坐标为31008. 如图,以点O为位似中心,将△ABC放大得到△DEF,若AD=OA,△ABC的面积为4,则△DEF的面积为( )
如图,以点O为位似中心,将△ABC放大得到△DEF,若AD=OA,△ABC的面积为4,则△DEF的面积为( )