题目内容
14.点P是直线y=-x+4上一动点,O为原点,则线段OP的最小值为( )| A. | 2 | B. | $\sqrt{2}$ | C. | 2$\sqrt{2}$ | D. | 4 |
分析 设直线y=-x+4与y轴交于点A,与x轴交于点B,过点O作直线AB的垂线,垂足为点P,此时线段OP最小,分别将x=0、y=0代入一次函数解析式中求出与之对应的y、x值,进而即可得出OA、OB的长度,利用勾股定理即可得出AB的长度,再利用面积法即可求出OP的长度.
解答 解:设直线y=-x+4与y轴交于点A,与x轴交于点B,过点O作直线AB的垂线,垂足为点P,此时线段OP最小.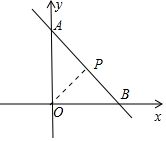
当x=0时,y=-x+4=4,
∴点A(0,4),
∴OA=4;
当y=-x+4=0时,x=4,
∴点B(4,0),
∴OB=4,
∴AB=$\sqrt{O{A}^{2}+O{B}^{2}}$=4$\sqrt{2}$.
∴OP=$\frac{OA•OB}{AB}$=2$\sqrt{2}$.
故选C.
点评 本题考查了点到直线的距离、一次函数图象上点的坐标特征、勾股定理以及三角形的面积,利用点到直线之间,垂直线段最短找出点P的位置是解题的关键.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案
相关题目
2.当a,b互为相反数时,代数式a2+ab-4的值为( )
| A. | 4 | B. | 0 | C. | -3 | D. | -4 |
4. 如图,抛物线y=ax2+bx+c(a≠0)与x轴一个交点为(-2,0),对称轴为直线x=1,则y<0时x的范围是( )
如图,抛物线y=ax2+bx+c(a≠0)与x轴一个交点为(-2,0),对称轴为直线x=1,则y<0时x的范围是( )
 如图,抛物线y=ax2+bx+c(a≠0)与x轴一个交点为(-2,0),对称轴为直线x=1,则y<0时x的范围是( )
如图,抛物线y=ax2+bx+c(a≠0)与x轴一个交点为(-2,0),对称轴为直线x=1,则y<0时x的范围是( )| A. | x>4或x<-2 | B. | -2<x<4 | C. | -2<x<3 | D. | 0<x<3 |
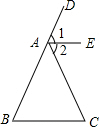 已知,如图∠B=∠C,∠DAC=∠B+∠C,AE平分∠DAC,AE∥BC吗?为什么?
已知,如图∠B=∠C,∠DAC=∠B+∠C,AE平分∠DAC,AE∥BC吗?为什么?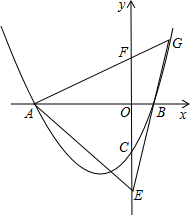 已知抛物线y=$\frac{1}{2}{x}^{2}+2mx-4m-2$(m≥0)与x轴交于A、B两点,A点在B点的左边.与y轴交于点C.
已知抛物线y=$\frac{1}{2}{x}^{2}+2mx-4m-2$(m≥0)与x轴交于A、B两点,A点在B点的左边.与y轴交于点C.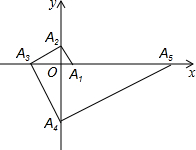 如图,点A1的坐标为(1,0),A2在y轴的正半轴上,且∠A1A2O=30°,过点A2作A2A3⊥A1A2,垂足为A2,交x轴于点A3,过点A3作A3A4⊥A2A3,垂足为A3,交y轴于点A4;过点A4作A4A5⊥A3A4,垂足为A4,交x轴于点A5;过点A5作A5A6⊥A4A5,垂足为A5,交y轴于点A6;…按此规律进行下去,则点A2017的横坐标为31008.
如图,点A1的坐标为(1,0),A2在y轴的正半轴上,且∠A1A2O=30°,过点A2作A2A3⊥A1A2,垂足为A2,交x轴于点A3,过点A3作A3A4⊥A2A3,垂足为A3,交y轴于点A4;过点A4作A4A5⊥A3A4,垂足为A4,交x轴于点A5;过点A5作A5A6⊥A4A5,垂足为A5,交y轴于点A6;…按此规律进行下去,则点A2017的横坐标为31008. 如图,以点O为位似中心,将△ABC放大得到△DEF,若AD=OA,△ABC的面积为4,则△DEF的面积为( )
如图,以点O为位似中心,将△ABC放大得到△DEF,若AD=OA,△ABC的面积为4,则△DEF的面积为( )